背包问题

背包问题通常分为两种类型：0-1背包问题和完全背包问题。

0-1背包问题：每个物品只能选择一次，即要么放入背包，要么不放入背包。
完全背包问题：每个物品可以选择多次，即可以放入背包多次。

0-1背包问题

/* 0-1背包问题 */
function 
    const n = w.length;
    const dp = Array.from({ length: n + 1 }, () => Array(C + 1).fill(0));
    for (let i = 1; i <= n; i++) {
        for (let j = 1; j <= C; j++) {
            if (j < w[i - 1]) {
                dp[i][j] = dp[i - 1][j];
            } else { 
                // 如果当前物品的重量小于等于背包的容量，那么有两种选择：放入或不放入背包 
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
            }
        }
    }
    return dp[n][C];
}

有个不好想到的点就是把容量全部拆解成从1开始累加1的序列, 而不是考虑实际物品的容量是不是以1为单位累加的.(这里的容易其实就是总重量), 所以有很大的存储空间浪费
先放第一个元素, 选出放还是不放入背包的最大值
如果选择不放, 则当前容量的值就是上一个元素对应容量的值dp[i-1][j]
如果选择放入, 则当前容量的值就是上一个元素对应容量减去当前物品重量的值dp[i-1]j-w[i-1]]加上当前物品的价值v[i-1]

核心难点是理解为什么不放入背包是dp[i-1][j-w[i-1]]+v[i-1]

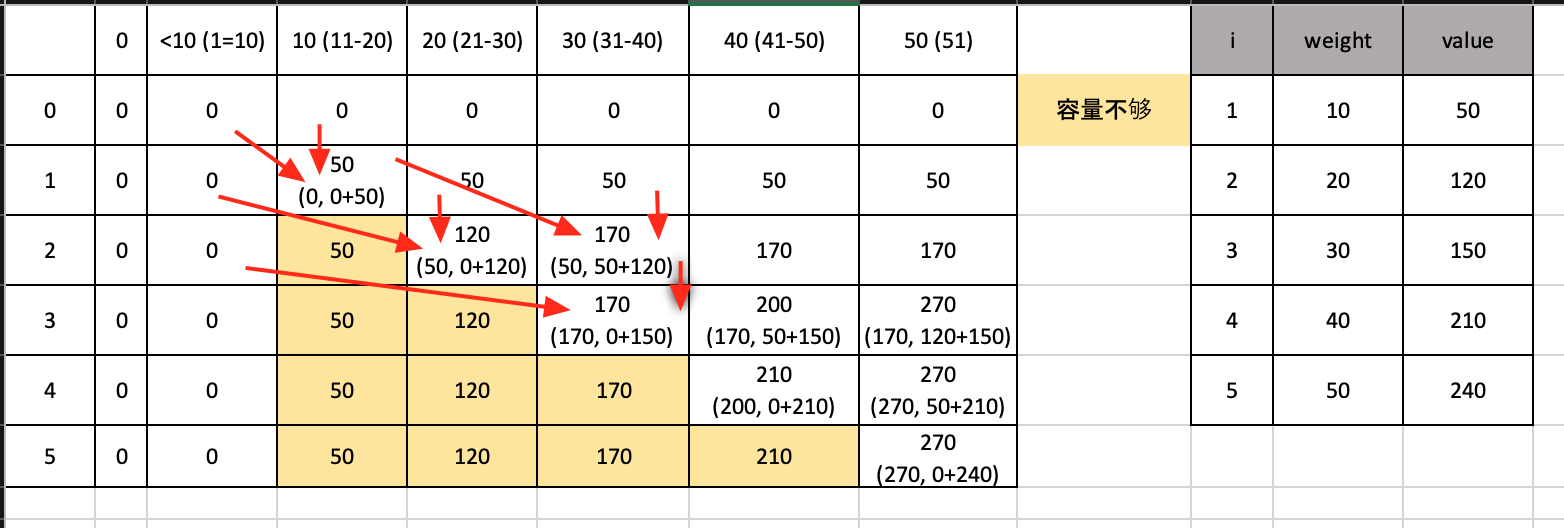可以看到, 每一个cell的状态来自于

它上面的一格
它左上角的"某"一格, 具体是哪一格, 取决于当前物品的重量

解说一下:

表格说明, X轴是代表容量, 因为这个例子是以10为跳跃和的, 所以我就每10个聚合在一起了, 又因为显示是以[i][j]这样的形式, 它们在数组上的意义比实际要多1, 注意必要的加减1的判断
X轴就是物, 1就是物品1, 所以取weight和value就要用[i-1]来取
放物品1的时候, 要直到容量到了10, 它的两个关联状态值都是0, 所以最大值显示就是自己, 50
- 容量继续增加没意义了, 因为它没有前序物品
物品2至少要容量到20才能到, 这时候, 一个关联状态值是50没问题, 左上角的关联状态值是多少呢? 显然, 因为如果要把自己放下, 物品1就放不下了, 那么至少得跑到<10那一列
- 观察下此时的变量: i=2, j=21, w[i-1]=20, j-w[i-1]=1, 列1处的值确实是0, 所以状态转移方程里, 放入自身元素, j的递减值, 就至少得是当前元素对应的weight值, 不管有多抽象, 表格里就是这样
从后续的例子里可以持续得到证明, 另一个关联状态的Y坐标确实是j-w[i-1]

其实就是如果要放下当前物品, 那么容量就要减当前物品的容量, 那么就要看缩减后的容量在上一个物品的最佳选择是什么, 也不是特难理解.

由于每个状态都只与其上一行的状态有关，因此我们可以使用两个数组滚动前进，将空间复杂度从 $O(n)$ 降至 $O(n^2)$ 。

压缩至一维数组:

/* 0-1 背包：空间优化后的动态规划 */
function knapsackDPComp(wgt, val, cap) {
    const n = wgt.length;
    // 初始化 dp 表
    const dp = Array(cap + 1).fill(0);
    // 状态转移
    for (let i = 1; i <= n; i++) {
        // 倒序遍历
        for (let c = cap; c >= 1; c--) {
            if (wgt[i - 1] <= c) {
                // 不选和选物品 i 这两种方案的较大值
                dp[c] = Math.max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
            }
        }
    }
    return dp[cap];
}

因为是不断改同一个数组, 如果你从前到后遍历, 那么低位的值改了后, 当前行还没遍历完, 但低位的值已经被改过了, 但是你倒序遍历的话, 高位的值改了不影响往低位遍历, 因为关联状态都在左上角. 所以要么倒序遍历, 要么用两个数组

完全背包问题

/* 完全背包问题 */
function knapsackCompleteDP(w, v, C) {
    const n = w.length;
    const dp = Array.from({ length: n + 1 }, () => Array(C + 1).fill(0)); // 初始化dp数组，dp[i][j]表示前i个物品放入容量为j的背包的最大价值
    for (let i = 1; i <= n; i++) {
        for (let j = 1; j <= C; j++) {
            if (j < w[i - 1]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - w[i - 1]] + v[i - 1]);
            }
        }
    }
    return dp[n][C];
    }

只有状态方程变了一点点：dp[i][j] = max(dp[i-1][j], dp[i][j-w[i-1]] + v[i-1])。仔细体会下, 0-1背包问题里, 如果要装下当前元素, 就要看压缩后的空间里上一个元素的最佳选择, 而完全背包问题下, 当前元素可以继续选择, 就从左上角选关联状态值变成了正左边.

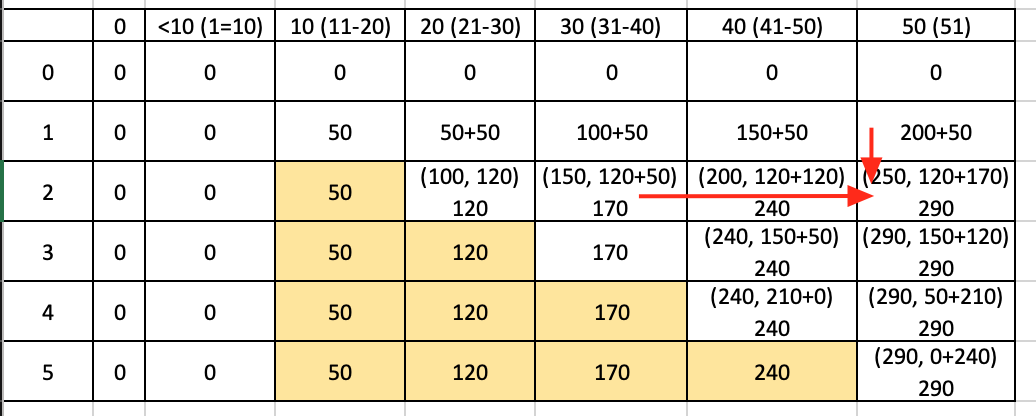
由于需要本行低位的最新值参与, 在完全背包问题的空间压缩的方案里, 就可以从前往后遍历了, 原因再重复一遍, 0-1问题里, 是有两个数组(一个表示上一行), 所以你不能更改需要用来比较的值, 而完全背包问题里, 比较的就是当前行.

/* 完全背包：空间优化后的动态规划 */
function unboundedKnapsackDPComp(wgt, val, cap) {
    const n = wgt.length;
    // 初始化 dp 表
    const dp = Array.from({ length: cap + 1 }, () => 0);
    // 状态转移
    for (let i = 1; i <= n; i++) {
        for (let c = 1; c <= cap; c++) {
            if (wgt[i - 1] > c) {
                // 若超过背包容量，则不选物品 i
                dp[c] = dp[c];
            } else {
                // 不选和选物品 i 这两种方案的较大值
                dp[c] = Math.max(dp[c], dp[c - wgt[i - 1]] + val[i - 1]);
            }
        }
    }
    return dp[cap];
}

零钱兑换

function coinChange(coins, amount) {
    const dp = new Array(amount + 1).fill(Infinity);
    dp[0] = 0;
    for (let i = 1; i <= amount; i++) {
        for (const coin of coins) {
            if (i >= coin) {
                dp[i] = Math.min(dp[i], dp[i - coin] + 1);
            }
        }
    }
    return dp[amount] === Infinity ? -1 : dp[amount];
}

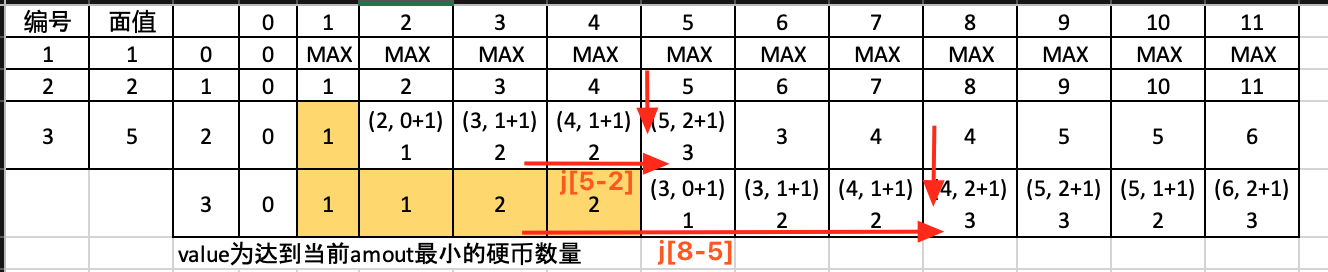从图中可以得出结论, 答案是3枚硬币

因为零钱可以重复使用, 所以是完全背包问题
值是硬币个数, 所以状态转移方程里加的不是当前的value, 而是当前硬币(即1)
初始化很重要, 金额为0时, 所需硬币都是0; 不用硬币时, 我们初始了个无穷大, 因为这样就能在min表达式中被忽略掉

也就是说, 只需要改两个位置:

初始值不是0, 是Infinity
状态转移方程里加的不是当前物品的value, 而是1

零钱兑换II

把问题由怎么兑换, 改为有多少种兑换零钱的方式, 建模上有多少变化?

初始值有变化, 没有硬币时兑换方式为0(即第一行是0); 金额为0时总有一种兑换方式(即0个硬币), 所以第一列是1
状态转移方程是累加前面的方案个数, 因为问的是多少种方案, 那么就是前面的方案, 加上如果把相应的数目的金额减掉, 改为当前硬币, 能符合要求的话, 有多少种方式, 所以是dp[i][j] = dp[i][j] + dp[i][j - coin]

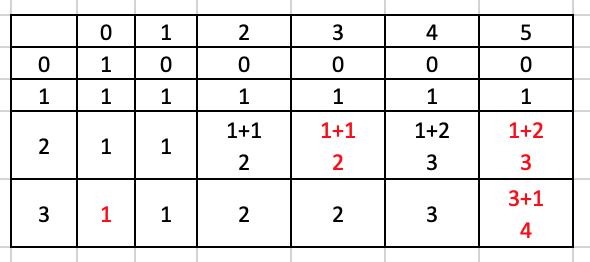
红字的格子即代表j-coin后来到的cell, 如5-2=3, 5-5=0
以(5,2)为例, 解是:1+2=3, 前面的1来自上一行, 说明不用2的情况下已有1个解能凑出5块
- 后面的2来自同一行, 说明有2种办法拼出3, 这样加上自己的2, 就是5

function change(amount, coins) {
    const dp = new Array(amount + 1).fill(0);
    dp[0] = 1;
    for (const coin of coins) {
        for (let i = coin; i <= amount; i++) {
            dp[i] += dp[i - coin];
        }
    }
    return dp[amount];
}

编辑距离问题

编辑距离，也称 Levenshtein 距离，指两个字符串之间互相转换的最少修改次数，通常用于在信息检索和自然语言处理中度量两个序列的相似度。

我没看懂, 先看教程里的分析:

要对齐是尾巴的e, 有三种方式, 直接添加,直接替换,和直接删除, 那就看组成前一截里的最小步骤, 似乎这个状态转移方程就出来了? 可是其中的"直接删除"要能生效, 依赖的是删除后的下一个字母就是e, 但看代码似乎是直接比较三种方案(其实是四种方案, 即如果两个字母刚好相等, 则不用操作), 那么如果删除后不是e, 那么这个方案不就失效了吗? 这个分支似乎应该要判断一下, 如果删除后是e, 则用这个方案, 否则用其他方案

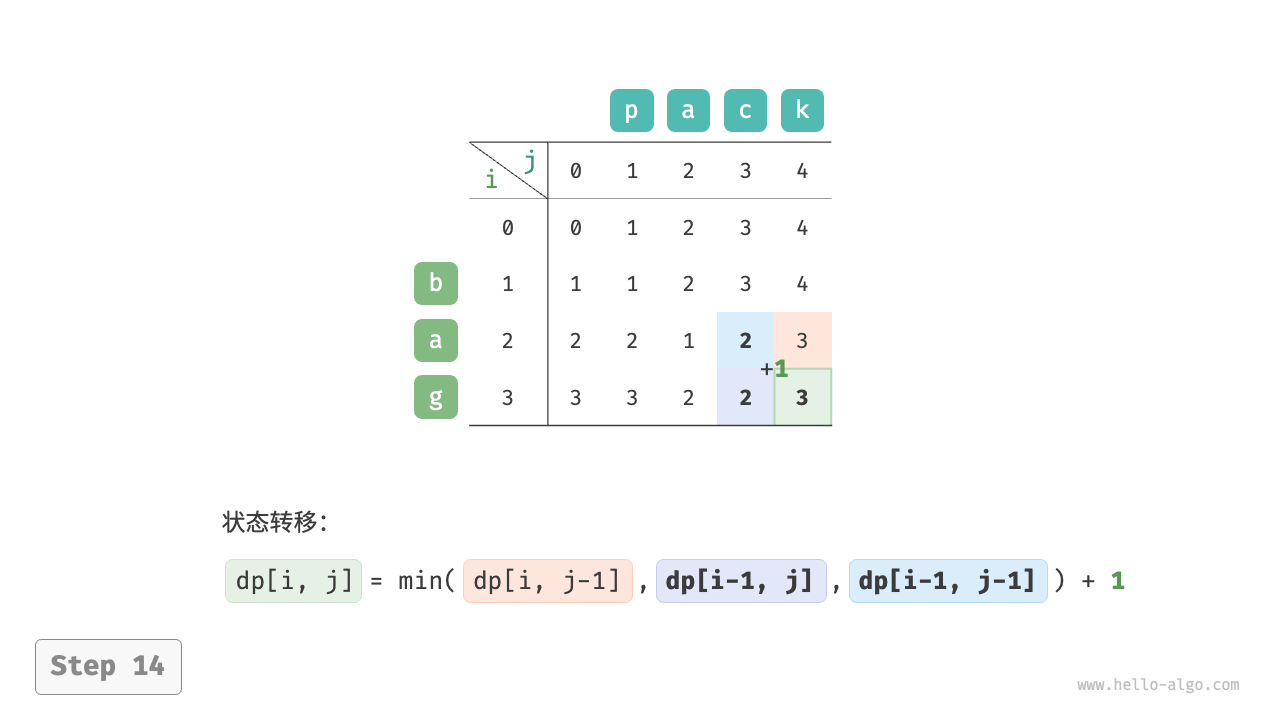如果不从模拟上去理解, 这个转移表格倒是简单, 我们已经反复做过这种表格了, 只是这次关联状态变成了它左, 上, 和左上三个cell里的值了, 其它思路都一样. 所以自己花点时间去理解这次这张表格是怎么画出来的吧.

/* 编辑距离：空间优化后的动态规划 */
function editDistanceDPComp(s, t) {
    const n = s.length,
        m = t.length;
    const dp = new Array(m + 1).fill(0);
    // 状态转移：首行
    for (let j = 1; j <= m; j++) {
        dp[j] = j;
    }
    // 状态转移：其余行
    for (let i = 1; i <= n; i++) {
        // 状态转移：首列
        let leftup = dp[0]; // 暂存 dp[i-1, j-1]
        dp[0] = i;
        // 状态转移：其余列
        for (let j = 1; j <= m; j++) {
            const temp = dp[j];
            if (s.charAt(i - 1) === t.charAt(j - 1)) {
                // 若两字符相等，则直接跳过此两字符
                dp[j] = leftup;
            } else {
                // 最少编辑步数 = 插入、删除、替换这三种操作的最少编辑步数 + 1
                dp[j] = Math.min(dp[j - 1], dp[j], leftup) + 1;
            }
            leftup = temp; // 更新为下一轮的 dp[i-1, j-1]
        }
    }
    return dp[m];
}

把道理讲明白, 那又得借助国外的教材了, 这里, 把abc转成yabd, 做矩阵, 它不是告诉你要初始化首行和首列为0,1,2,3,4, 而是先各加一个空字符串, 意思是整个表都是怎样把左侧的字符串转成右侧的字段串

空转空, 所需的步骤是0, 空转y, 所需的步骤是1, 转ya, 需要两步, 以此类推, 第一行的1234的来由
第一列, 仍然是左转右, 空转空, 是0, a转空, 要1步, ab转空, 要2步, 以此类推

小结: 横向和竖向后面的字符串是累积的, 所以如果不让人迷惑, 写成"", y, ya, yab, yabd会更好理解. 我推荐所有的教程都用这种写法, 而不是一次一个字母, 在脑袋里累积.

\begin{array}{c|ccccc} & \tt""& p& pa& pac& pack \\ \hline \tt""& 0& 1& 2& 3& 4 \\ b& 1& 1& 2& 3& 4\\ ba& 2& 2& 1& 2& 3 \\ bag& 3& 3& 2& 2& 3 \end{array}

随机取几个值验证下:

ba转成"", 需要两步, 删除b和a
ba转成p, 同理, 先删除一个字母, 再替换一个字母, 两步
ba转成pack, b转成p, 添加c和k
- 它所有的可选方案就是左上角的所有可能性(哪怕最极端的, 退回空串, 再依次添加), 显然, 选最贴近的三个方案做比较就好了, 没必要退得那么远
- 周边最小的步骤是2, 也就是说, ba到pac最少需要2步, 即删除a, 然后添加c

忽略这些实际场景, 那就是(i-1, j-1), (j, j-1), (i-1, j)三个值里选最小的, 然后加1, 就是期望的最小步骤了.

Backlinks

《Hello算法》学习笔记 (learning)