Machine Learning Basic

PCA

source

Principal Conponent Analysis using Singular Value Decomposition (SVD)

用图表我们最多能表达3个维度的特征：

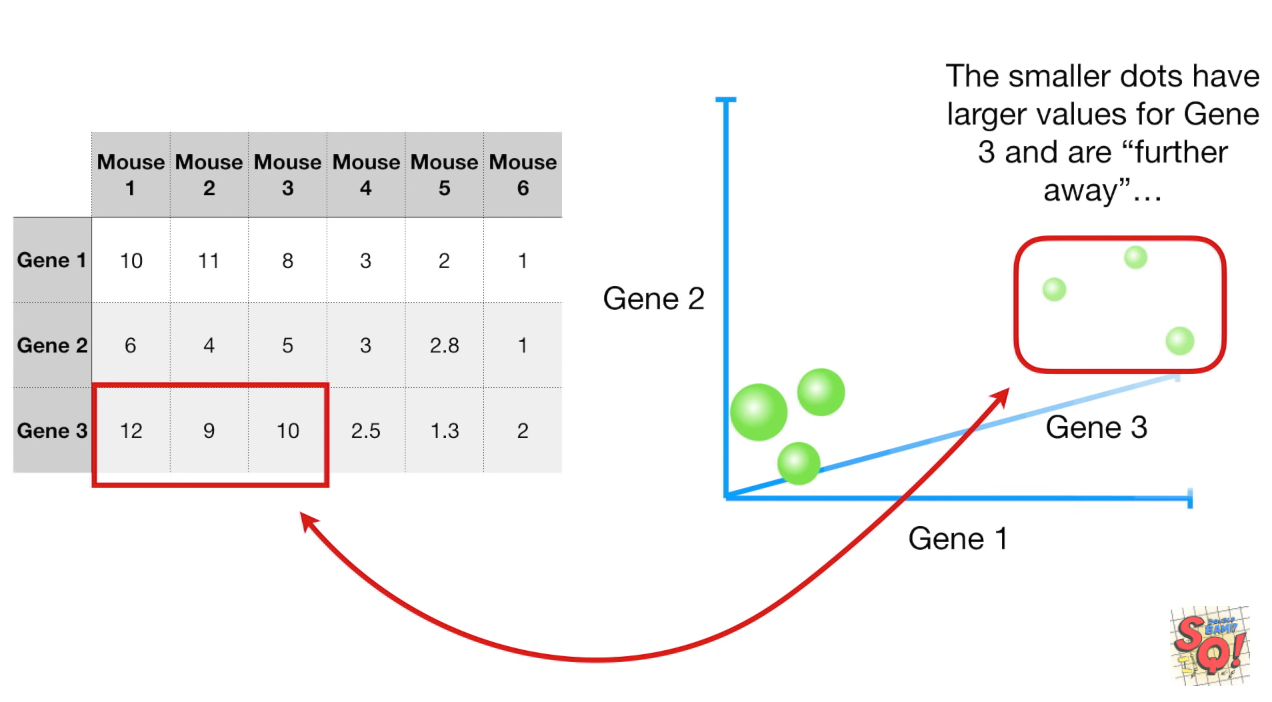
更多的话已经无能为力了，现在我们回到2维特征，

• 绘图后，把x值取个中值，y值也取个中值，得到一个center，我们就把center理解为所有数据的中点
• 再把中点移到原点
• 进现在所有的点进行回归（必须过原点？）

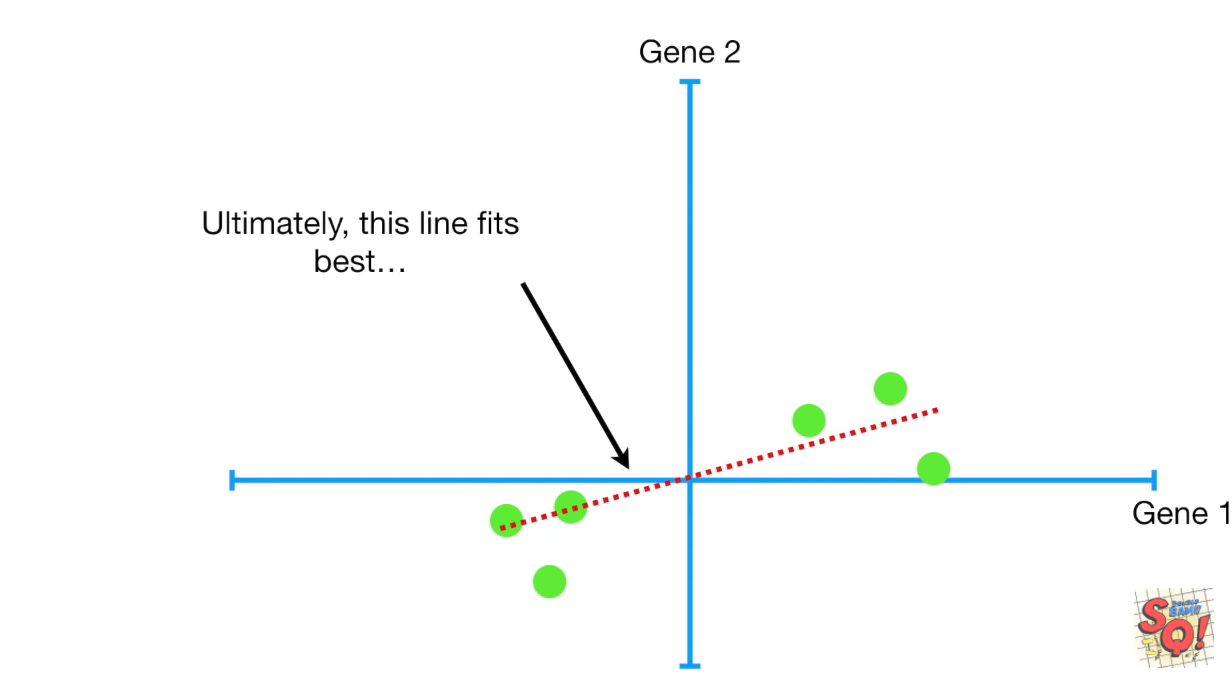
不是回归这么简单，为了衡量这条线有多fit这些数据点，我们把数据点投影到线上。

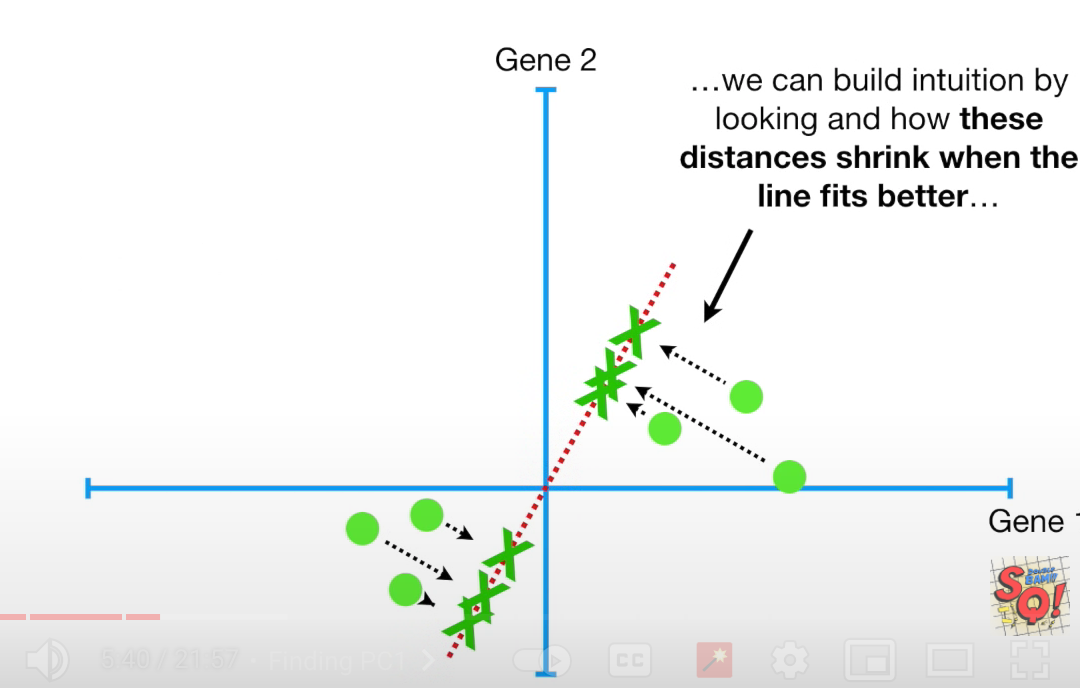
现在有两个判断指标（作用是一样的）：

• 每个点到线的投影的垂直距离之和，最长，fits best
• 每个点在线上的投影到中心的距离之和，最短，fits best

从勾股定理能知道，

• 斜边（就是向量本身，即点的位置）不变，设为a，
• 投影垂直距离为b
• 投影到中心（原点）的距离为c

a是不可能变的，那么b和c就是负相关的关系了。

PC1

我们来计算所有的投影到中心的距离之和： $ SS(distance) = c_1^2 + c_2^2 + \cdots + c_6^2 $ 得到SS的最小值，对应的线我们称为Principal Copmponet 1 (PC1), 如图

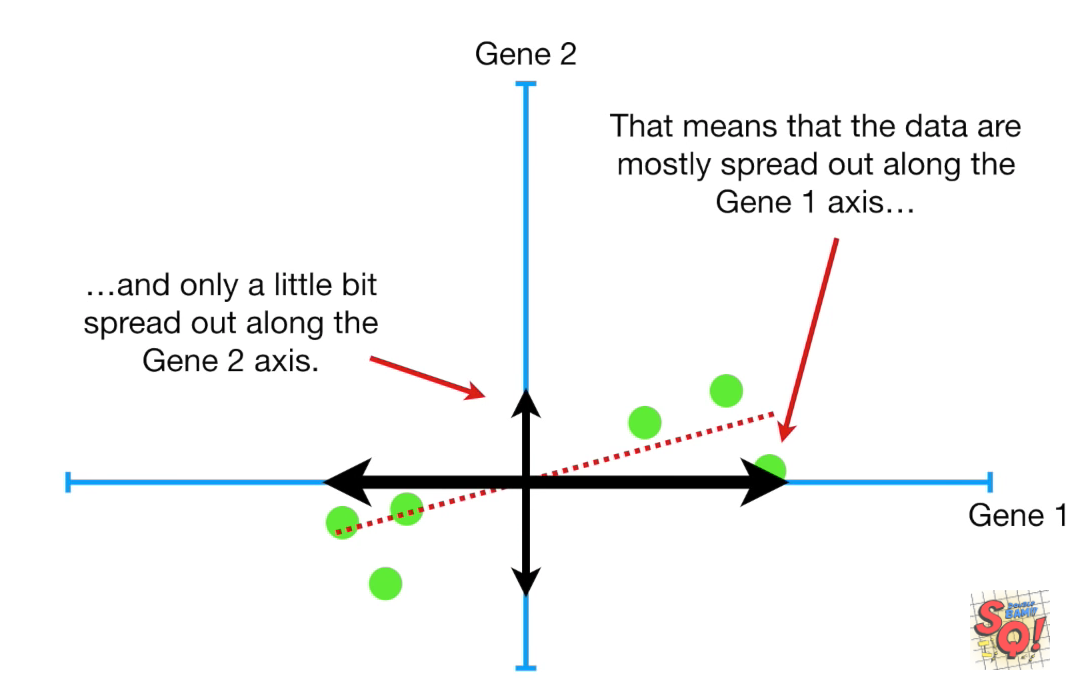它是一条斜率为0.25的过原点的线，也就是说，它在x轴上的延展是4倍于y轴上的延展（数据的分布）

也可以理解为要构成PC1，需要4份x，1份y。(x是gene1, y是gene2)

或者说，

• PC1是x和y的线性组合(linear combination ) $\larr$ 术语1
• 而线性组合就是矩阵啊

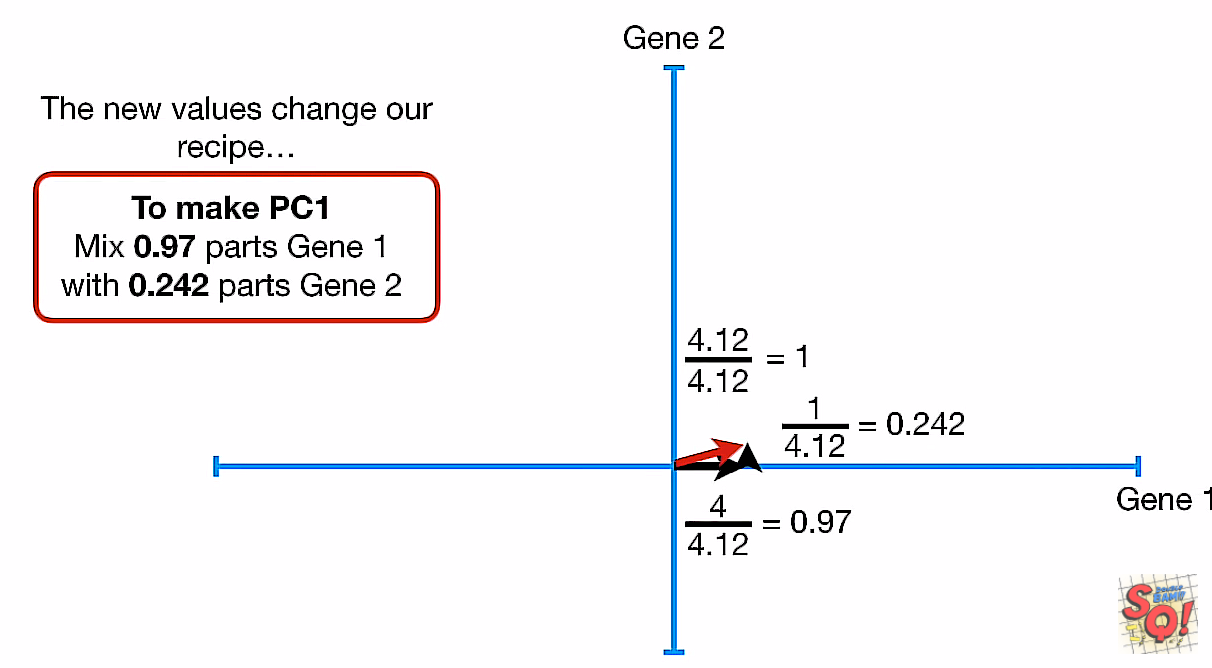
继续应用勾股定理，并归一化（既在PC1这条线上找到单位长度的向量，开始计算）

• 前提是我们知道了线性组合是1:4，那么：$4^2 + 1^2 = length^2$
• $lentgh = \sqrt{17} \approx 4.12$
• 归一化后 length = 1, -> (a, b) = ($\frac{1}{4.12}$, $\frac{4}{4.12}$)
• (0.242, 0.97)
• 那个PC1上的单位长度的向量我们称为Sigular Vector或Eigenvector for PC1 (就是矩阵的eigen value) $\larr$ 术语2
• 再取根号：$\sqrt{Eigenvalue\ for\ PC1}$ = Singular Value for PC1 = SS(distances)
• 所以我们把Singular Value给分解成(0.242, 0.97)这个过程就叫奇异值分解(SVD)？

PC2

我们对PC1从原点做一条垂直线，可知斜率变成了(-4)，分解的值为(-0.242, 0.97)

• 同样，可以理解为对投影到PC2来说，gene2有4倍重要于gene1
• 但Eigen Value of PC2不再是投影距离的平方和，而是中心距离的平方和了

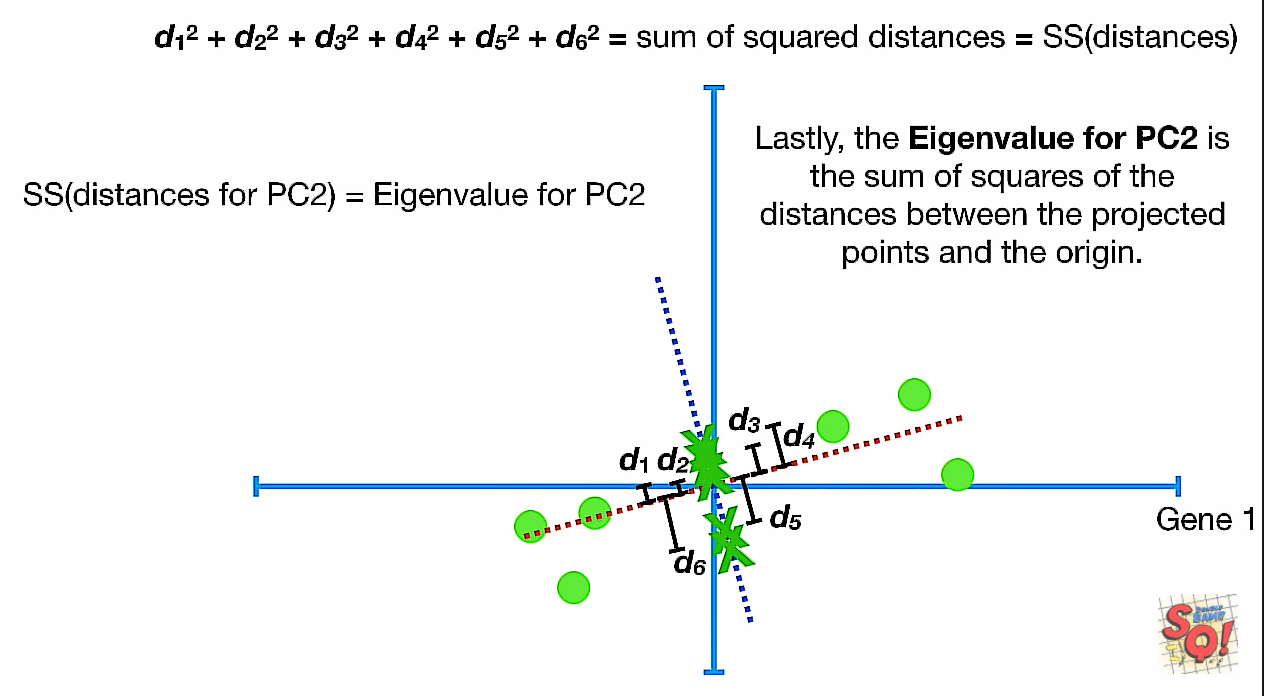
这时候我们就要问了，为什么要一个垂直的PC2？

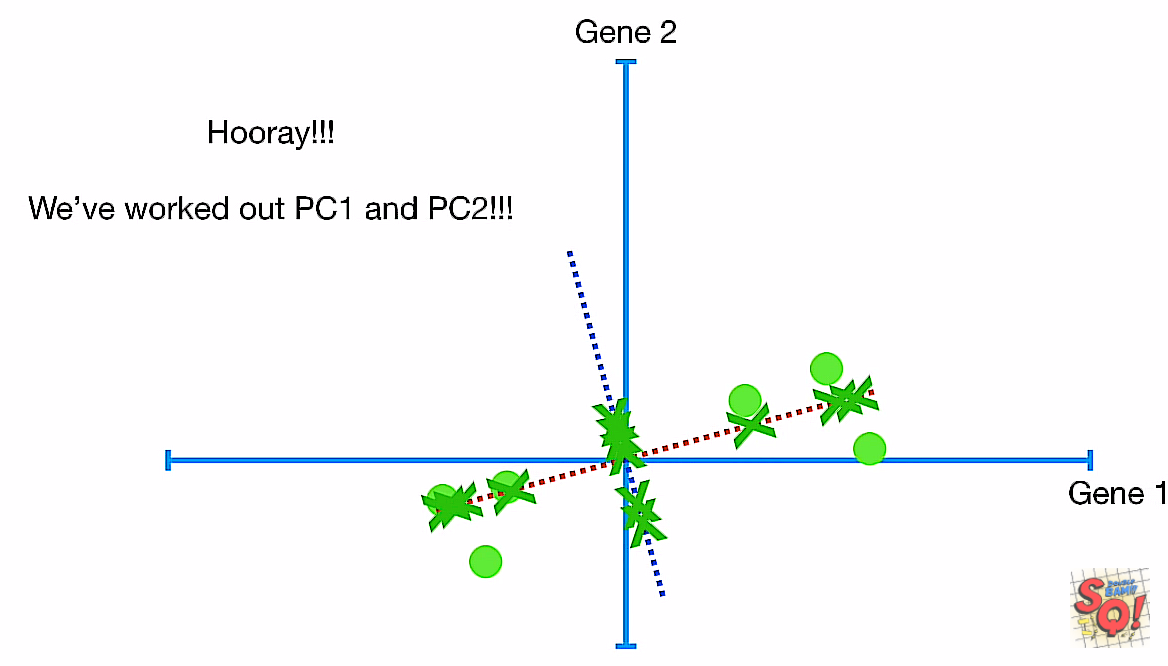
有没有发现，PC1和PC2已经组成了自己的坐标系了！！！只要再把它旋转一定的角度。

投影到两条轴上的点分别成了新的x，y坐标，成点：

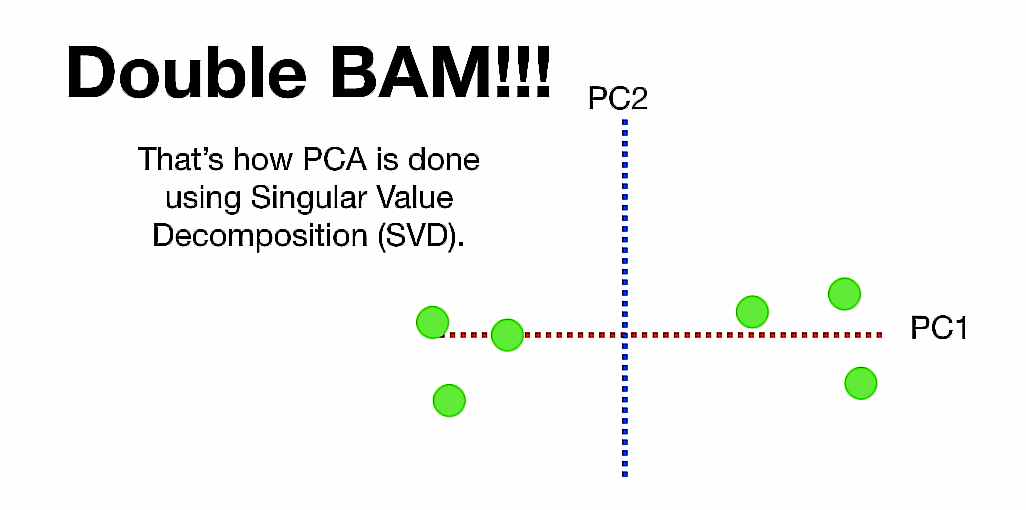
这个时候，我们之间讨论的两个度量：

1. 投影距离
2. 投影与中心的距离 分别就成了y值和x值

Scree Plot

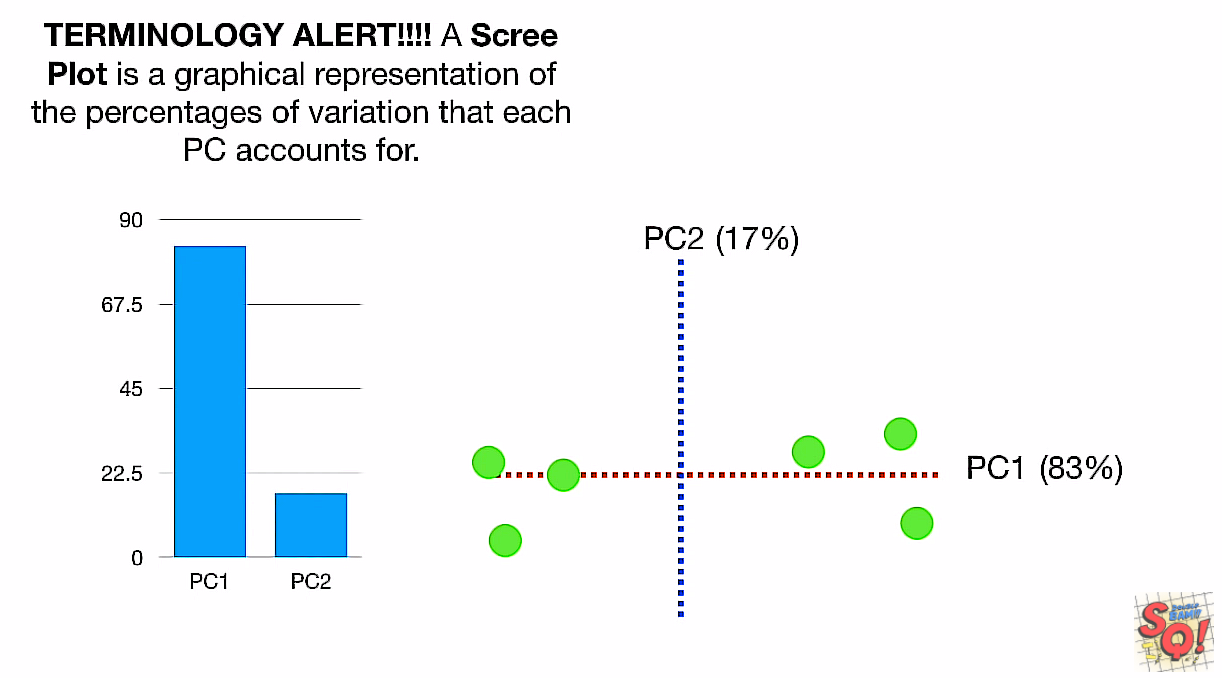
不知道PC1的83%哪来的！！！（好像是用ss(distance)的比例）

降维

终于来到高维了，用三维举例（仍能画图）。

• 找到中点
• 移到中点
• 找到best fitting line
• 算出linear combination
• 归一，得到(0.62, 0.15, 0.77)

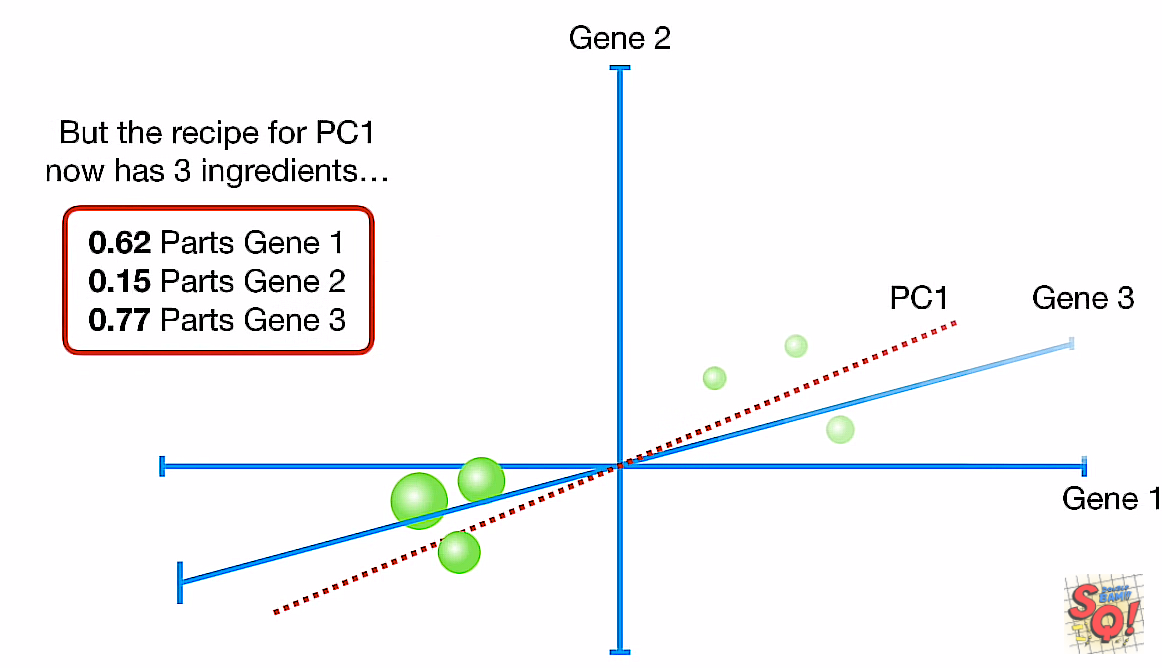
这个时候我们就要想了，PC2怎么选，不像在二维平面直接对PC1画条垂线就有了的。

没讲怎么来的，也说是best fitting line，怎么可能正好是垂直于PC1?） -> 难道是说有条件的best fitting? 比如一定要垂直于PC1?

以此类推，还能找到一条PC3，互垂于前两条（这里是讲得最糊的地方，如果是要垂直于既往的线的次优解，那么先找pc2还是pc3可能会有差别）

并且也没讲第三条线是用最大投影长度还是用最小中心距离（前面说的pc1用投影长度，pc2用中心距离）

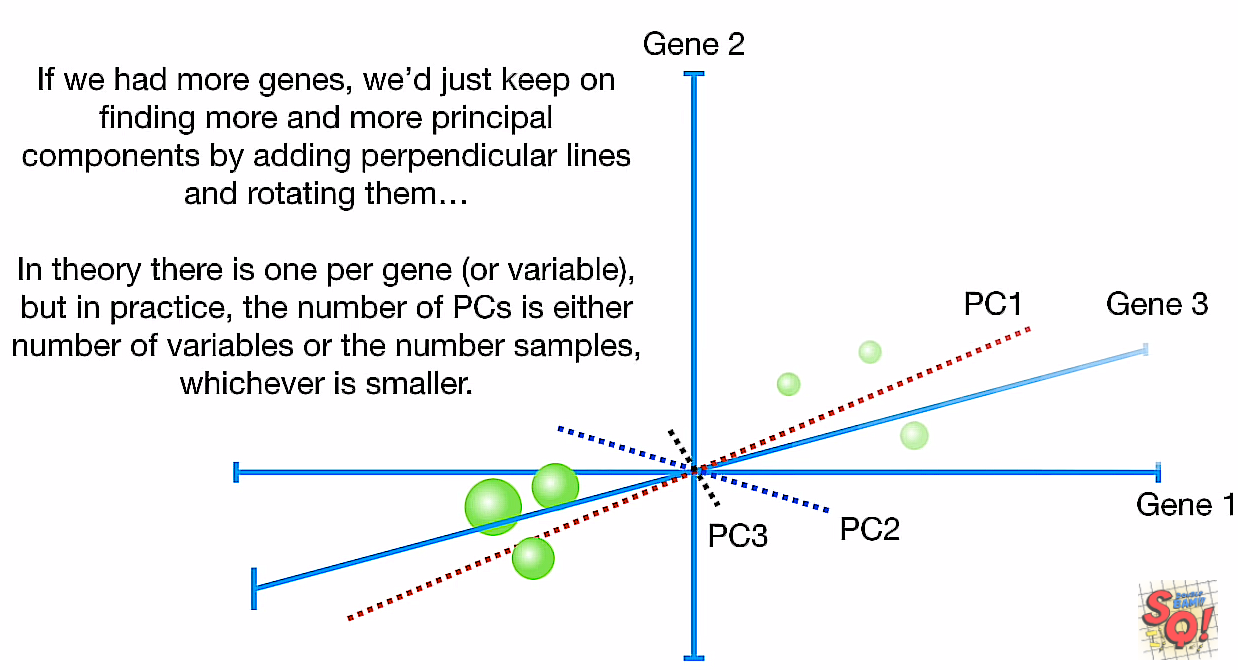
variation又来了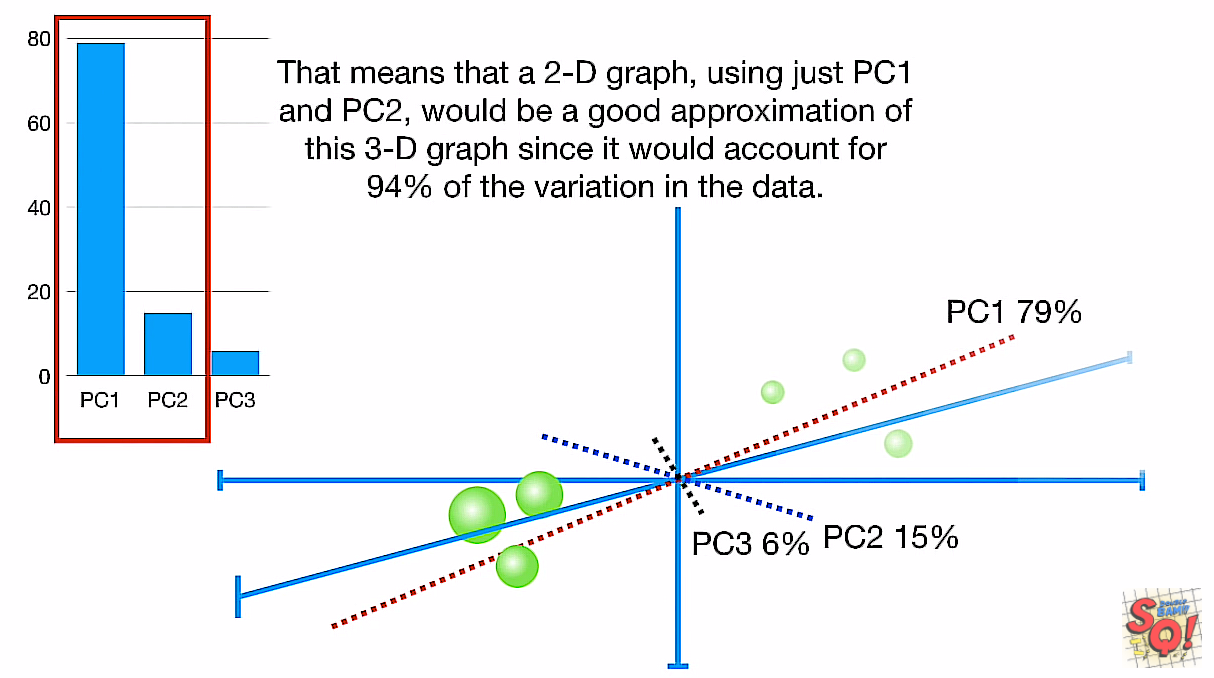： 确定只需要pc1和pc2就占了大部分，就选择这两个维度来当坐标系。

分别投影到两条轴上：

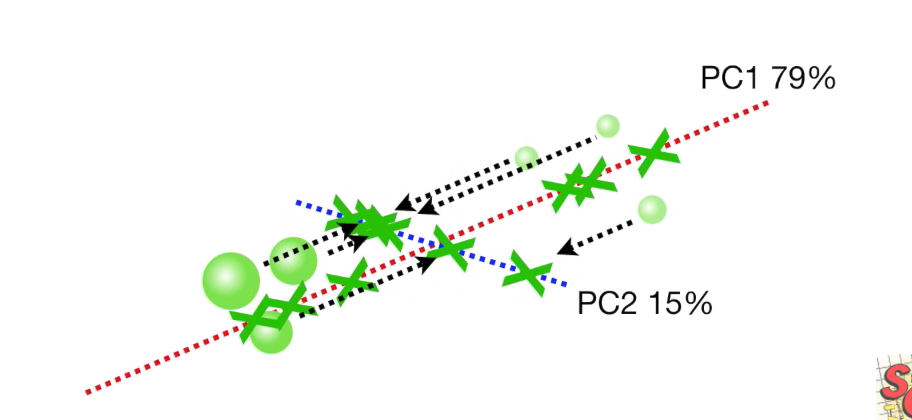
finally：

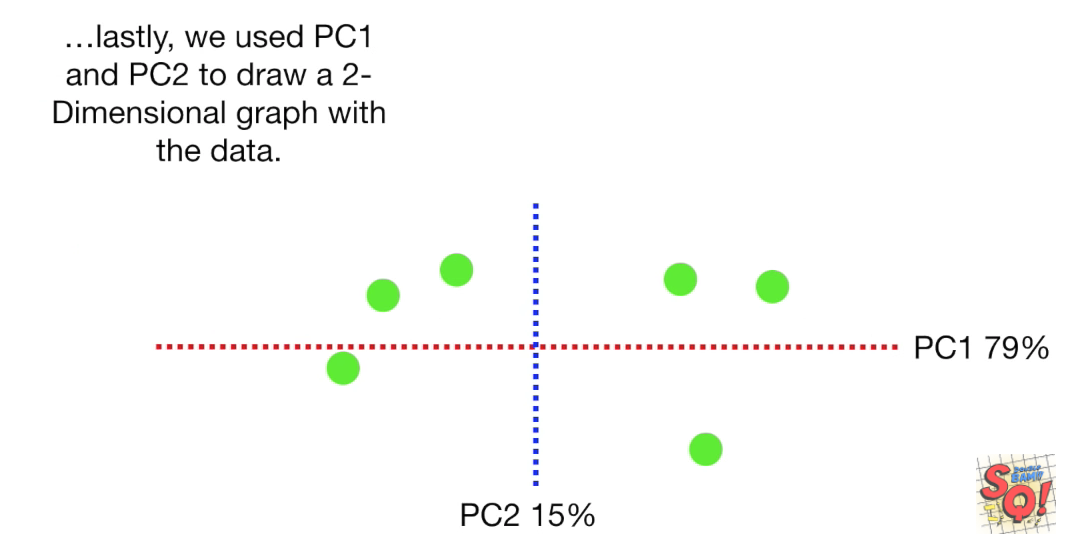
更高维

再高维就不能绘图了，然而已经不重要了。

绘图是为了帮助理解，以上的best fitting line的计算，全是通过数学（或现成的库）计算出来的，而不是绘出来的，升到4维，并没有什么变化。

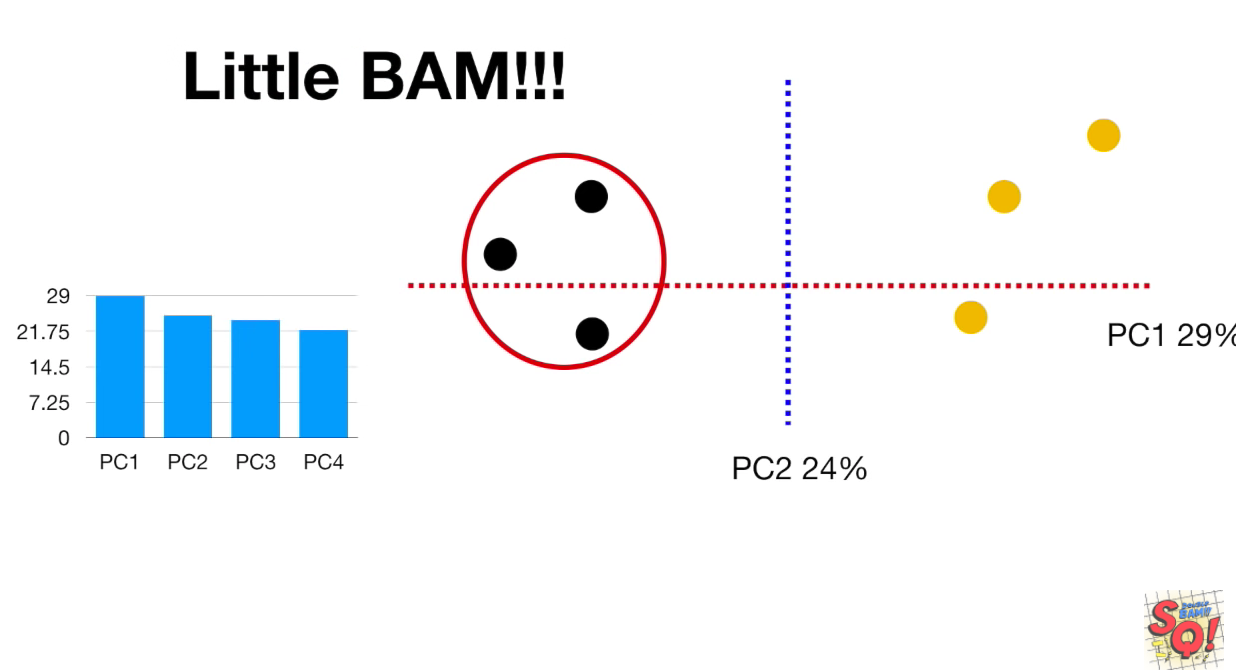
如果几个pc的variation差不多，我们还能只取前两个吗？

取了后就成了聚类的效果了。

Math

直接从数学上来解释就是把轴画在了方差最大的方向，如果是多维的，就是协方差：

• $\bar X = \frac{\sum_{i=1}^NX_i}{N}$
• $S = \frac{\sum_{i=1}^N(X_i - \bar X)^2}{N -1}$
• $C = \frac{\sum_{i=1}^N(X_i - \bar X)(Y_i - \bar Y)}{N-1}$ $\larr$ 协方差矩阵

将数据转换为只保留前N个主成分的特征空间的伪代码如下所示：

• 去除平均值
• 计算协方差矩阵
• 计算协方差矩阵的特征值和特征向量
• 将特征值排序
• 保留前N个最大的特征值对应的特征向量
• 将数据转换到上面得到的N个特征向量构建的新空间中（实现了特征压缩）

LDA

线性判别式分析(Linear Discriminant Analysis, LDA)是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。

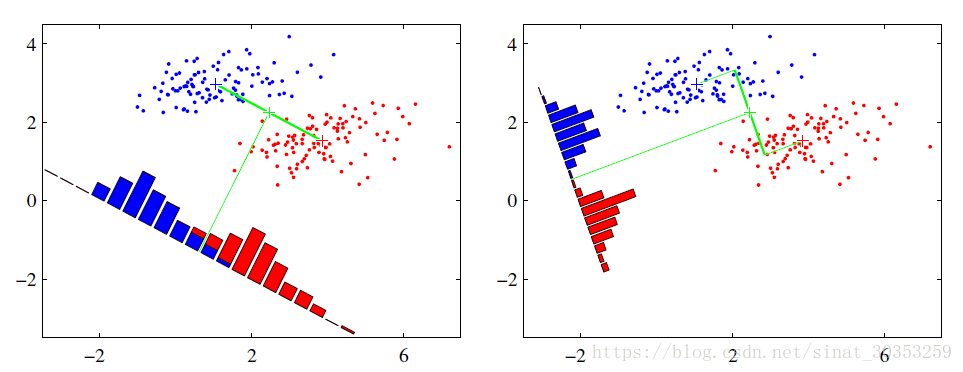
算法

...

集成学习

提升算法（AdaBoost）

AdaBoost的实现是一个渐进的过程，从一个最基础的分类器开始，每次寻找一个最能解决当前错误样本的分类器。

用加权取和(weighted sum)的方式把这个新分类器结合进已有的分类器中。

它的好处是自带了特征选择（feature selection），只使用在训练集中发现有效的特征(feature)。

这样就降低了分类时需要计算的特征数量，也在一定程度上解决了高维数据难以理解的问题。

最经典的AdaBoost实现中，它的每一个弱分类器其实就是一个决策树。这就是之前为什么说决策树是各种算法的基石。

装袋算法（Bagging）

同样是弱分类器组合的思路，相对于Boosting，其实Bagging更好理解。

它首先随机地抽取训练集（training set），以之为基础训练多个弱分类器。

然后通过取平均，或者投票(voting)的方式决定最终的分类结果。 因为它随机选取训练集的特点，Bagging可以一定程度上避免过渡拟合(overfit)。

Stacking

在多个分类器的结果上，再套一个新的分类器。这个新的分类器就基于弱分类器的分析结果，加上训练标签(training label)进行训练。一般这最后一层用的是LR。

提醒说stacking在数据挖掘竞赛的网站kaggle上很火，相信参数调得好的话还是对结果能有帮助的。