Array

Static and Dynamic Arrays

static array

• fixed length
• indexable

usage:

• sequential data
• IO routines as buffers
• lookup tables and inverse lookup tables
• return multiple values

operation complexity: access: O(1) search: O(n) insert: O(n) append: O(1) delet: O(n) 需要遍历的操作就是O(n)

Q: How to implement a dynamic array? A:

1. static array with an initial capacity
2. add new elements, keep tracking the size
3. if exceed capacity, create a new static array with twice the capacity
   • and copy the original elements into it

Singly and Doubly Linked Lists

单向/双向链表

sequential list of nodes that hold data which point to other nodes also containing data.

• 节点序列，
• 节点拥有指向别的节点的数据（指针）
• 别的节点也拥有这种指针

usage:

• many List, Queue & Stack implementations
• circular lists
• model real world objects such as trains
• implementation of adjancy list for graphs
• separate chaining -> ?
  • deal with hashing collisions -> ?

上述两上问号后续在Hash Table一节里自然就解惑了

Terminology Head / Tail / Pointer / Node

Singly vs Doubly

• Doubly holds a next and prev reference, which Singly has no prev
  • 插入删除的时候需要更新所有引用
• both maintain a reference of head and tail for quick additions / removals

insertion

• create a traverser and move by sepcific steps
• create new node
• singly:
  • 原node的next指向新node
  • 新node的next指向原next的node
• doubly:
  • 新node的next和prev分别指向原node和下一个node
  • 两个node分别用next和prev指向新node

removal

singly需要两个游标:

• pt1指向head, pt2指向head->next
• pt1, pt2一起移动，直到pt2找到目标
• pt2再向前移动一步
• pt1位置的node用next指向pt2位置
• now can sefely remoing the element between pt1 and pt2

doubly却只需要一个：

• pointer找到目标元素
• 用prev和next找到上一个和下一个
• 下一个和下一个node分别互相指向

Complexity searth: O(n) insert at head/tail: O(1) remove at head: O(1) remove at tail: O(n) (singly) / O(1) (doubly) 因为即使我们知道tail在哪，在单向链表中，我们也找不到它的前一个去设置为新的tail remove in middle: O(n)

Stack

• one-ended linear data structure (LIFO)
• two operation: push and pop

Usage

• undo mechanisms
• compiler syntax checking for matching brackets and braces
  • 开括号压入栈内，每碰到一个闭括号，与栈顶的比较，匹配就出栈，不匹配就报错
• model a pile of books or plates
  • 汉诺塔(tower of hanoi)
• tracking previous function calls
• DFS on a graph

Complexity push/pop/peek/size: O(1) search: O(n)

双向链表实现一个Stack，基本上就是操作tail

Queues

• a linear data structure, model real world queues (FIFO)
• two primary operations: enqueue, dequeue

Usage

• any waiting line models a queue
• keep track of the x most recently added elements -> ?
• web server request management where you want first come first serve
• BFS graph traversal

Complexity

只有contains, revomval需要遍历，其它操作（出入列等）都是O(1)

实现一个BFS： 基本就是动态往 queue 里添加子节点,当前级别元素访问完后, 再 dequeue 出来的就是所有的下一级子节点

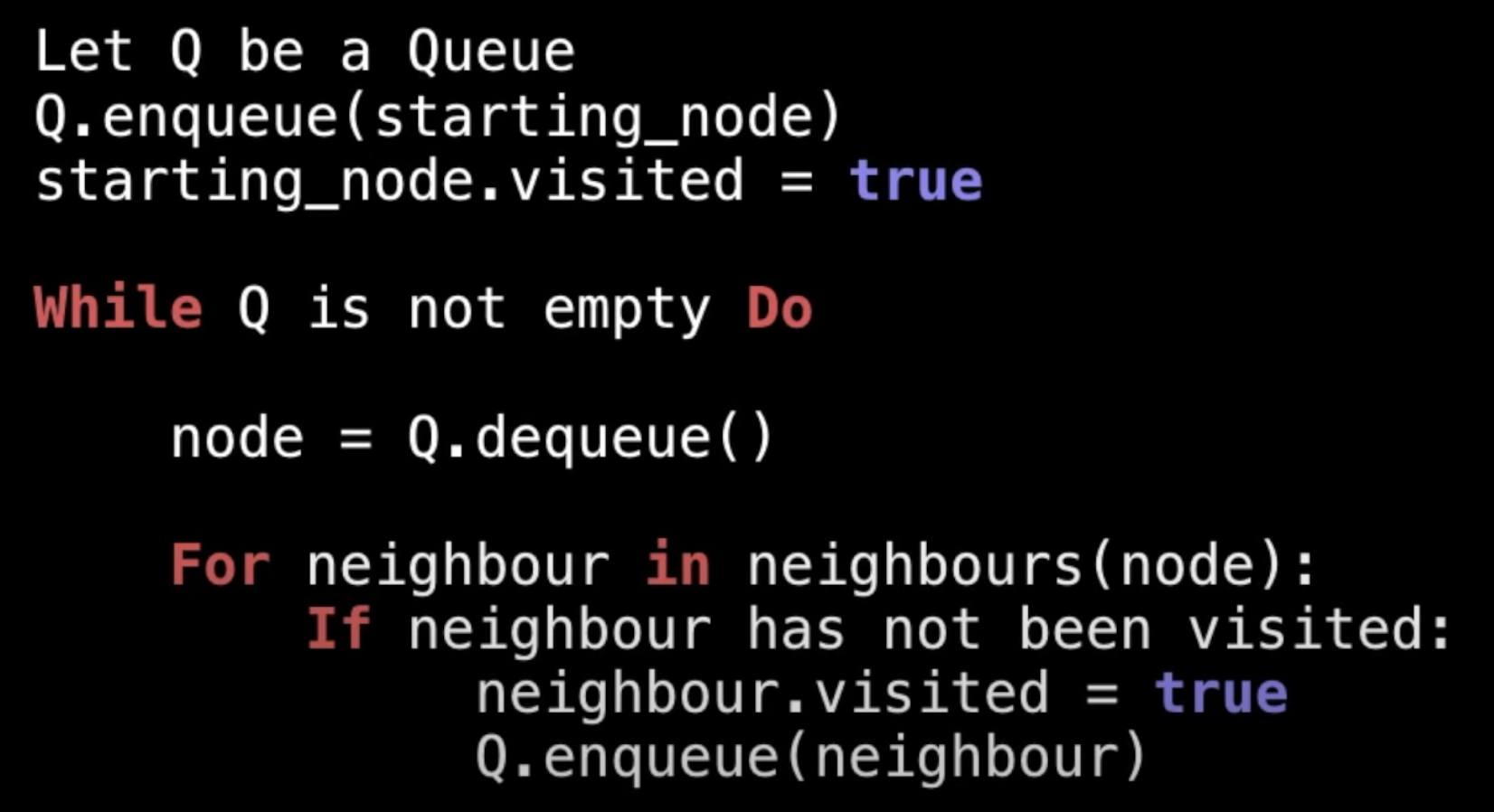
双向列表实现Queue，入列用tail，出列用head，即添加的总在尾巴，永远从头部取出。

Priority Queues (PQs) with an interlude on heaps

• A priority queue is an Abstract Data Type (ADT)
• except each element has a certain priority
  • determine the order (removed from the PQ)
• need comparable data

每次取出最小（或最大）的->pool，添加到PQ，如何得知极值呢？-> heap

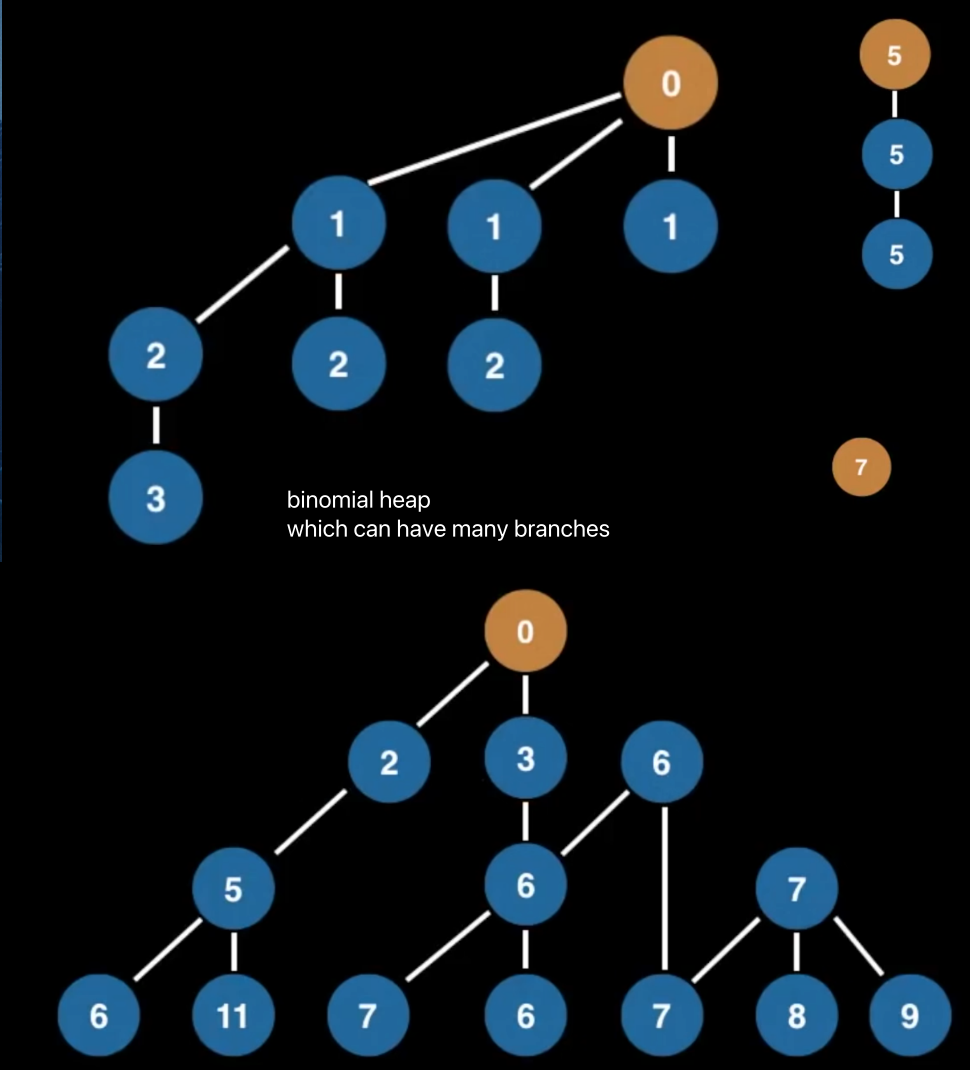
Heap

• a tree based data structure
• statisfies the heap invariant(heap property):
  • if A is a parent node of B then A is ordered with respect ot B for all nodes A, B in the heap
  • 说人话，A是B的父节点，如果A比B大，那么比B的所有子节点都大，vice versa

Priority Queue有时候也被叫做Heap，因为它只是一个ADT，当然它也可以用别的数据结构实现。

以下四个，都是heap 这些就不是

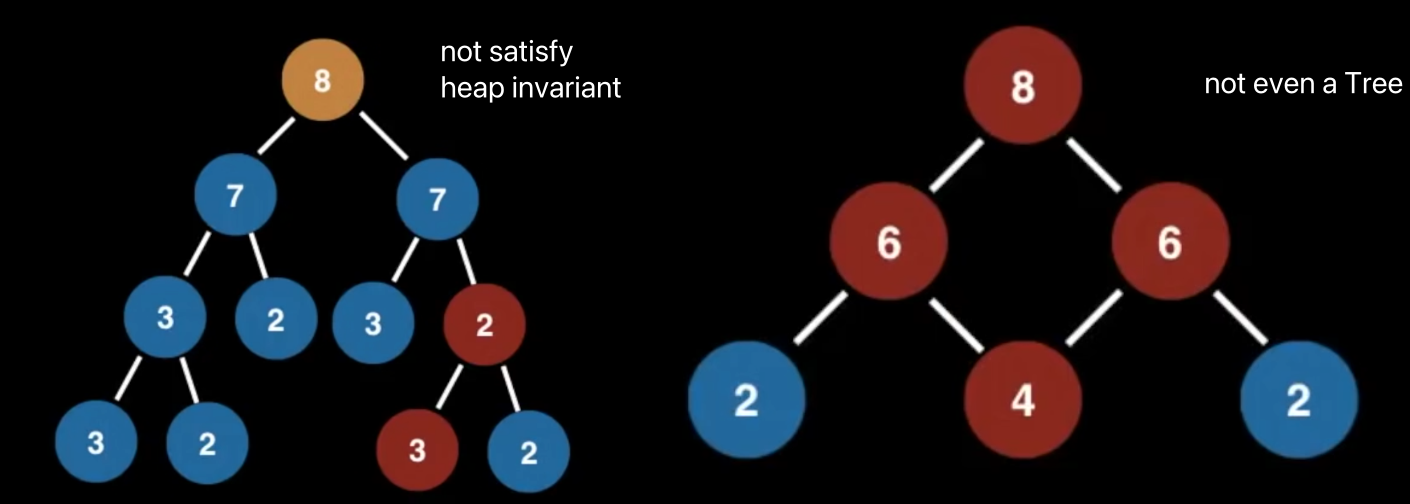
Usage

• certain implementations of Dijkstra's Shortest Path algorithm
• anytime you need the dynamically fetch the next best or worst element
• Huffman coding -> lossless data compression
• BFS，PQs continuously grab the next most promising node
• Minimum Spaning Tree (MST) algorithm

可见是很多算法的基础

Complexity

• Binary Heap construction: O(n)
• Polling: O(log n)
• Peeking: O(1)
• Adding: O(log n)
• 原生删除：O(n)
  • with hash table: O(log n)
• 原生contains: O(n)
  • with hash table: O(1)

Turning Min PQ into Max PQ

大多数编程语言标准库只提供了min PQ。

1. 在构建min pq的时候，把比较标准从x>=y变成x<=y（operator重载）
2. 在构建min pq的时候，把x变成-x，取出的时候再取反一次

原则都是取巧，而且，第二种方法，存在pq里的，并不是你要使用（和本想存储）的对象，所以取出的时候需要处理。

Priority Queue with Binary Heap

实现了heap invariant的binary tree.

除了Binary Heap，还有很多

• Fibonacci Heap
• Binomial Heap
• Paring Heap
• ... 都能实现一个PQ

Adding Elements to Binary Heap

• 从尾部(last leaf)添加
• 如果违反了heap invairant(即比parent大)，则交换
• 向上冒泡

Removing Elements From a Binary Heap

1. Poll()

• 因为root总是优先级最高的元素，poll移掉的就是root
• root当然不能直接移，所以先跟最后一个元素swap
• swap后原root就没有children了，直接移除
• 最低优先级的元素到了top，所以要向下冒泡
  • 先左后右，先低再高
  • 即如果两个子级优先级一样，那么直接与左边交换
  • 否则哪个优先级最低就与哪个子级交换
  • 子级优先级都比它低，就完成了pool()

2. Remove(m) 即删除一个特定元素

• linear scan，找到元素位置
• 与last node交换，然后移除
• last node用先上向下的原则冒泡
  • 即先看能不能往上冒泡，不能的话再看往下冒泡

Complexity Pool(): O(log n) Remove(): O(n) (最坏情况下，可能要删的元素在最后一个)

用hashtable优化remove

• hashtable为lookup和update提供constant time
• 因为为Index和value建立了映射，这样不需要通过遍历，直接通过映射就能找到元素
  • 如果两个node拥有同样的value呢？
  • 直接把每个value对应的n个索引全部存起来(set)
  • 但我应该remove哪一个呢？
    • 随便，只要最终satisfy the heap variant

Union Find

• keep track of elements in different sets
• primary operations: find and union

Usage

• Kruskal's minimum spanning tree algorithm
• Grid percolation
• Network connectivity
• Least common ancestor in trees
• Image processing

Complexity

• construction: O(n)
• union/join/size/check connected/: $\alpha$(n) :接近常量时间
• count: O(1)

给定一个无向图，如果它任意两个顶点都联通并且是一棵树，那么我们就称之为生成树(Spanning Tree)。如果是带权值的无向图，那么权值之和最小的生成树，我们就称之为最小生成树(MST, Minimum Spanning Tree)。 -> 用最少的边连接所有的顶点

• sort edges by ascending edge weight
• walk through edges
  • 检查顶点，如果两个顶点都已经unified，就忽略
    • 其实就是这两个点分别被别的边连过了
  • 否则就添加edge，并且unify顶点

看到这里，首先想知道什么是unified，看实现，也就是在一个集合里(component)

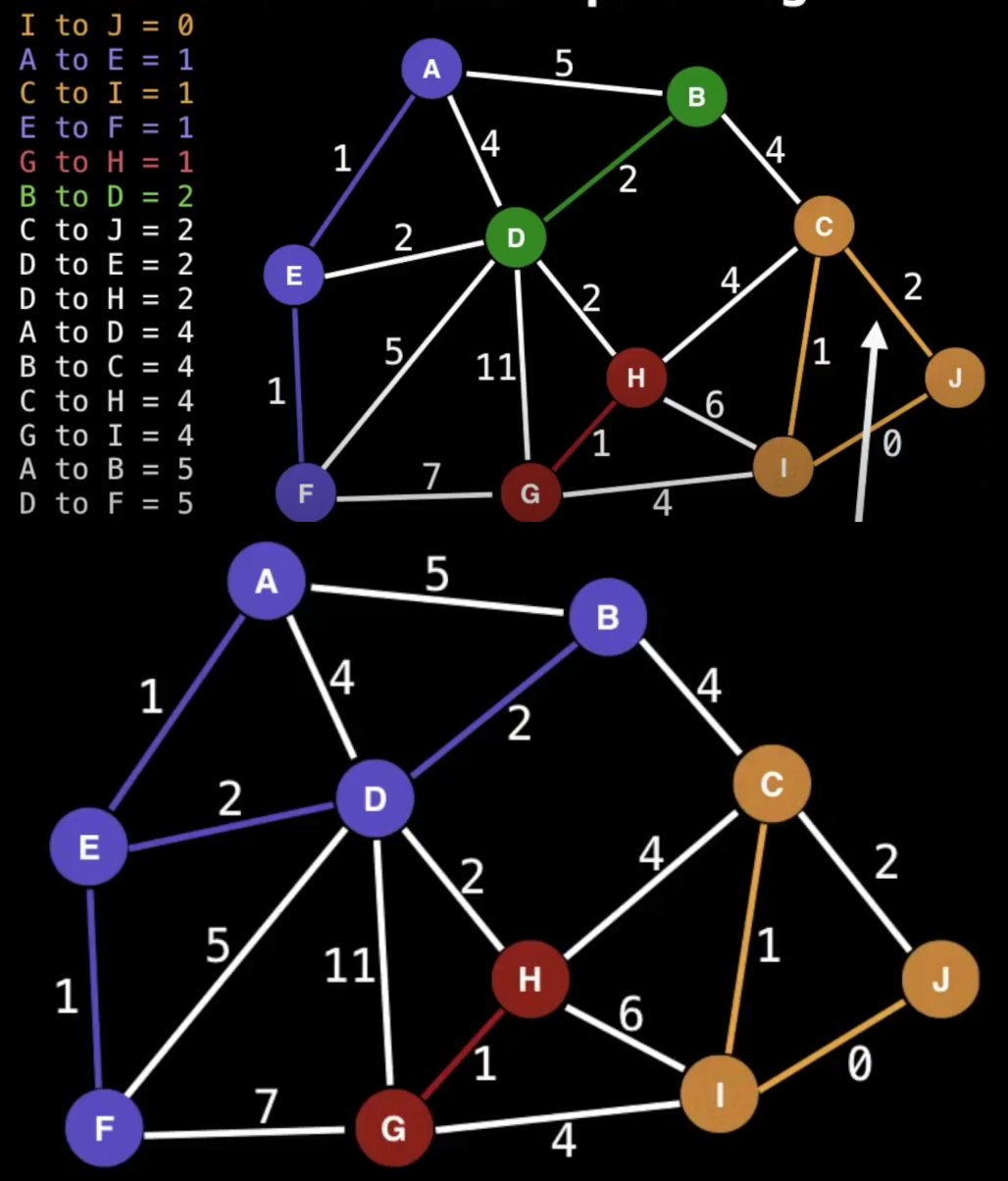
• 观察C_J，因为C和J已经在一个组里了，这条边就不需要了
• 观察D_E，一旦连上后，紫色和绿色其实就是一个组了
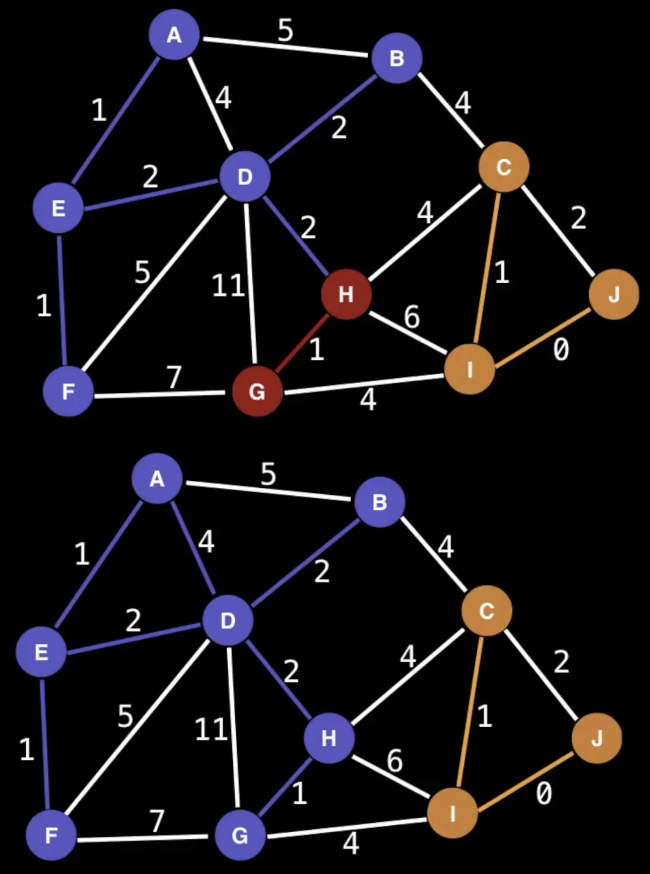
• 观察D_H，一旦连上后，紫色和红色也成为了一个组
• 连接B_C，所有顶点就全部连上了，并且只有一条紫线

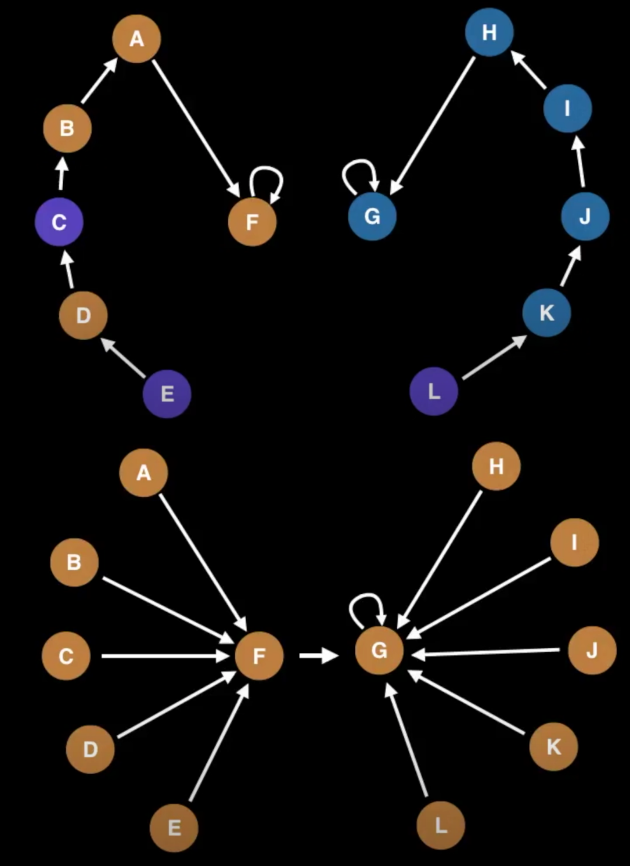
Find: 找元素在哪个component里，然后找到它的root Union: 找两个元素分别在哪个component里，然后找到它们的root，如果不是同一个root，就让其中一个成为另一个的parent

• component的个数与root的个数一致
• root的个数只减不增（因为通常只合并而不拆分）

union find里

• 为每个元素分配一个索引，每个元素指向自己（即初始是n个root，n个component)
• 描述两两之间的关系，以任一元素为parent （谁来描述？）
• 有一个元素已经属于别的component里的，就将它也加到那个component里去
  • 如果这个元素也是别的component里的顶点，就把整个组指向另一个组的root

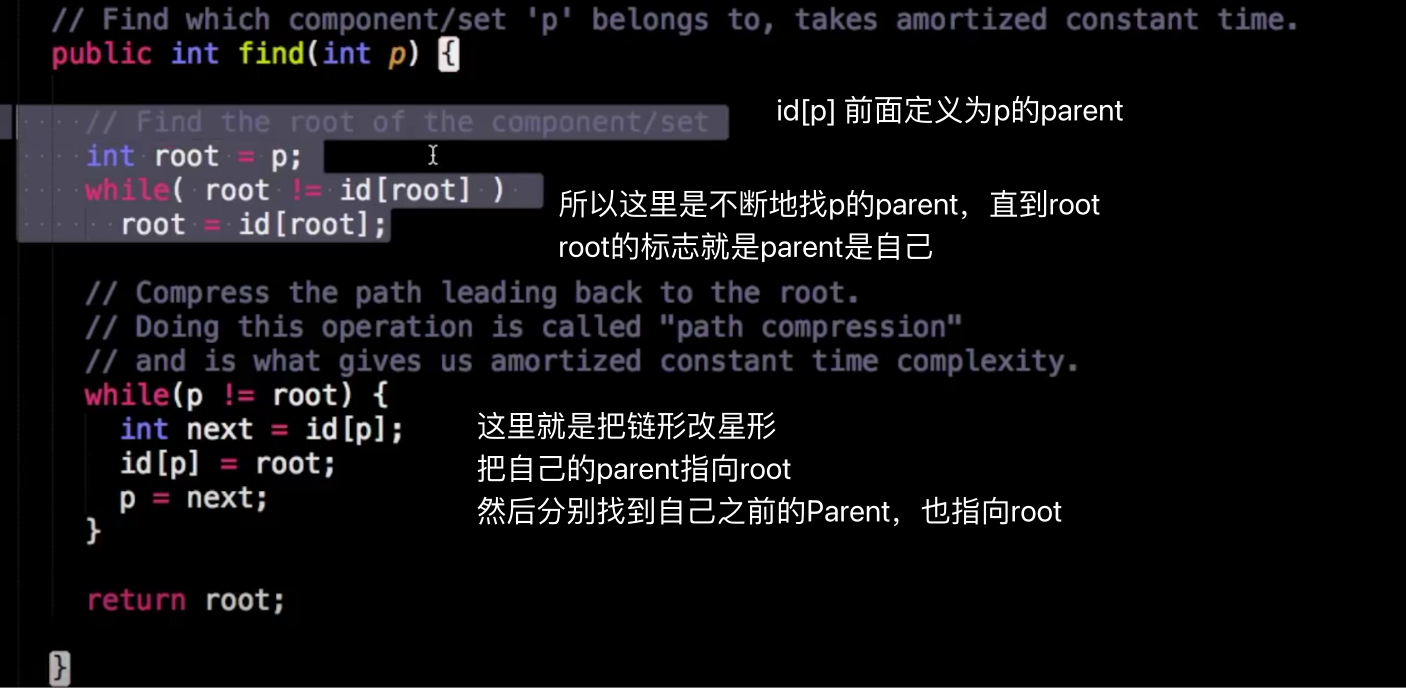
Path Compression Union Find

由一层层找到root改为所有顶点直接指向顶点（星形结构），实现路径压缩

这段代码演示的是，查找p的root节点，在查找的过程中，顺便进行了路径压缩

合并的逻辑就是比较谁的元素多就把谁当作root，另一个component的root的parent设为元素多的组的root
合并完成后组数就少了1 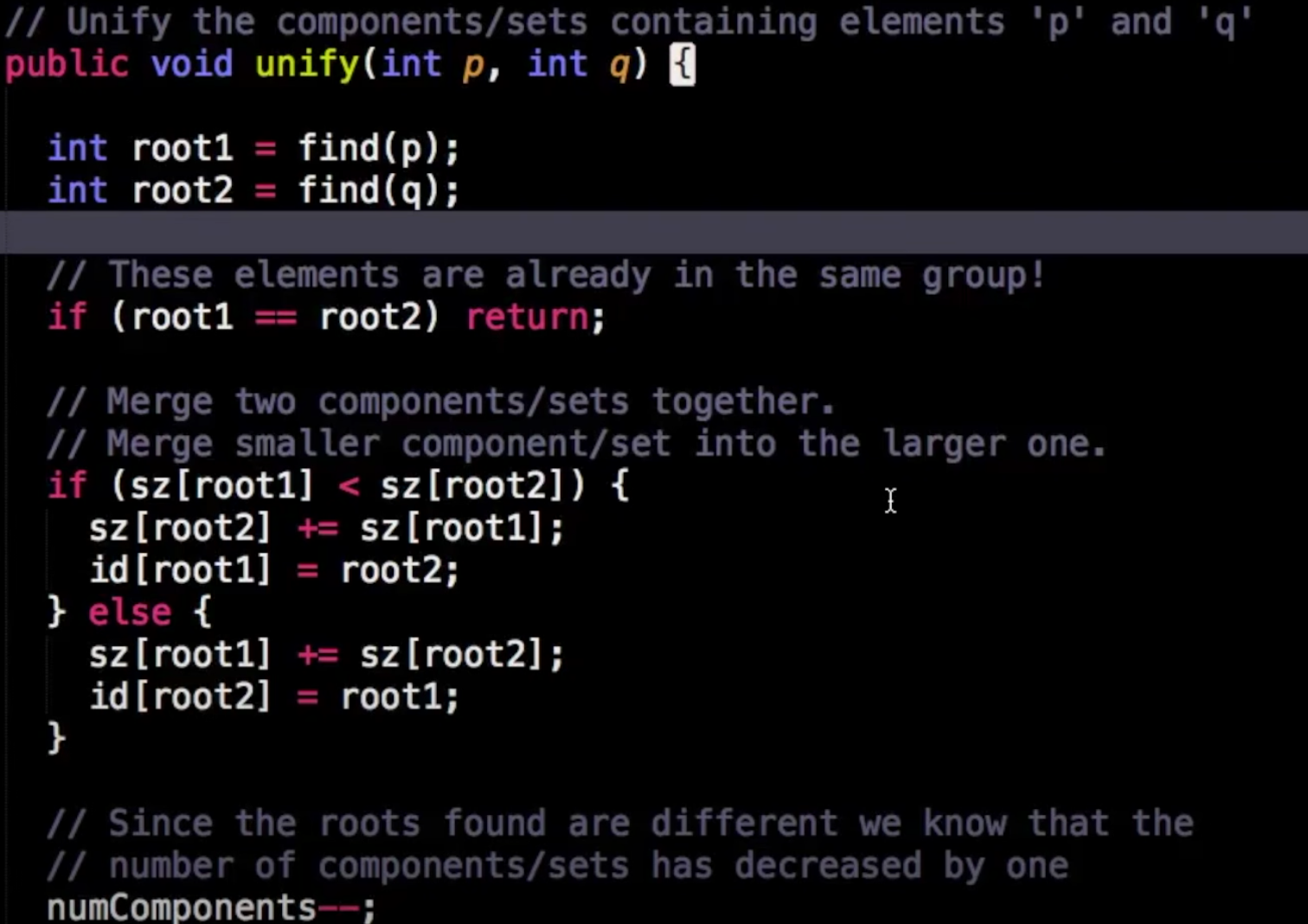看代码，这一步里面并没有路径压缩，也就是小组里面的元素并没有进一步再星状地指向新的parent，仍然指向的是老的组的root

Binary Trees and Binary Search Trees (BST)

Tree: 满足以下定义的undirected graph(无向图)

• An acyclic(非循环的) connected graph
• N nodes and N-1 edges
• 有且只有一条路径连接任意两个顶点

任意一个节点都可以被理解为root

Binary Tree 拥有最多两个节点的Tree

Binary Search Tree 服从以下特性的binary tree

• 左子树的元素小于右子树

拥有重复元素是允许的，但多数情况下我们只研究不重复的元素

这是一个有效的BST吗？

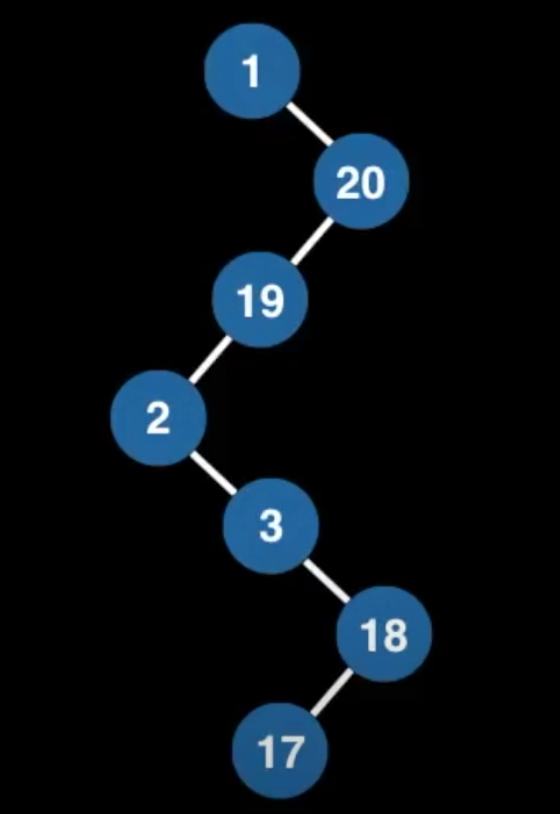
是的（对于单链下来的，几乎会直接就满足右边比左边大）

Usage

• BSTs
  • implementation of some map and set ADTs
  • red black trees
  • AVL trees
  • splay trees
  • ...
• binary heaps
• syntax trees (by compiler and calculators)
• Treap - a probabilistic DS (uses a randomized BST)

Complexity 增删查平均为O(log n)，但最差情况下都为O(n)，即线性时间

Adding elements to a BST

• 第一个为root
• 每一个新数，比顶点大，放右边，比顶点小，放左边，顺序下行
  • 不是从左到右摆满再做subtree
  • 比如3,6,9, 会得一棵全部数字摆在右边的数，而不是顶3左6右9的三角形
  • 这也是为什么极端情况下，时间复杂度是O(n)，因为就是一条线到底
  • 这也是balanced binary search trees被引入的原因

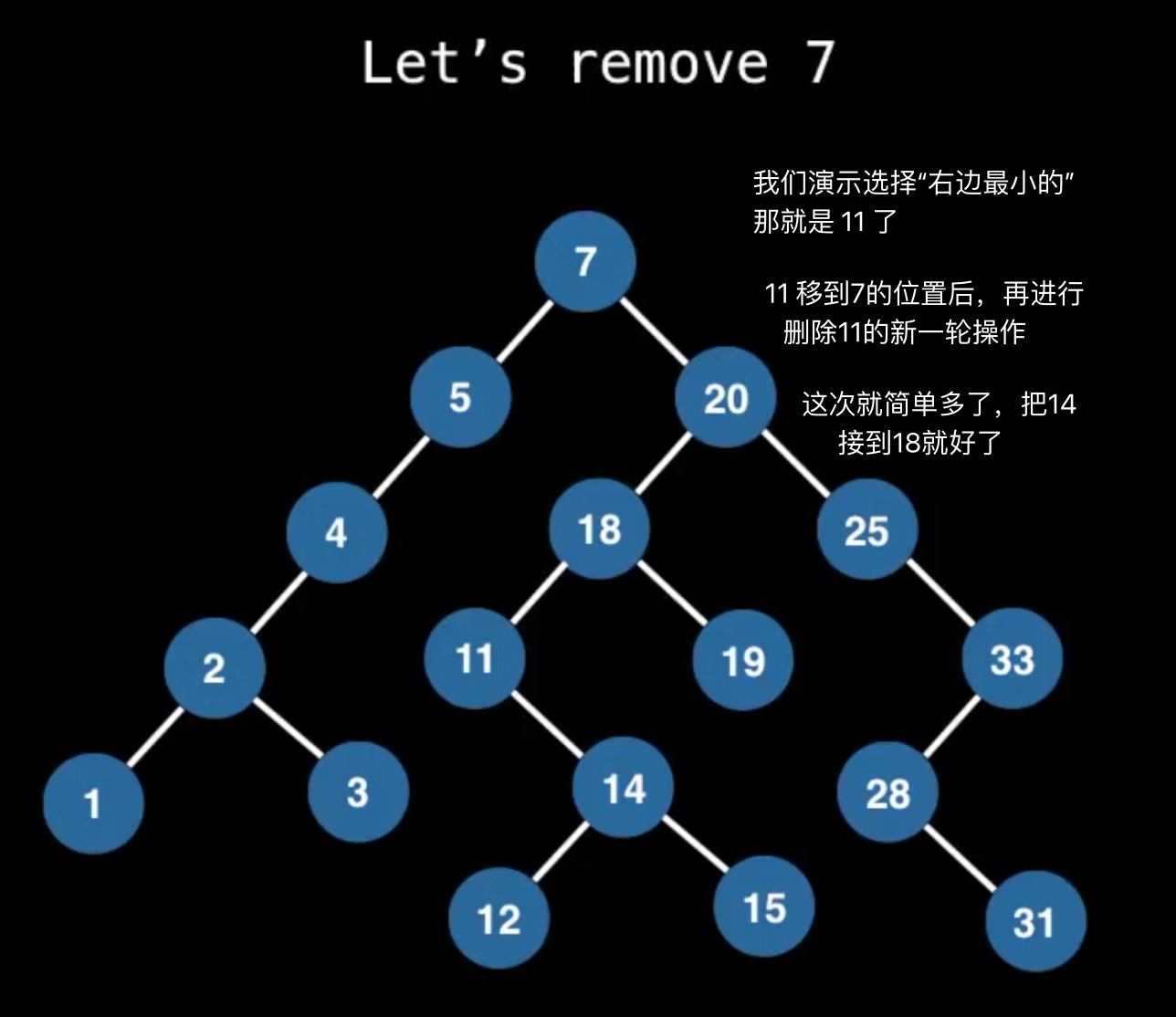
Removing elements from a BST

• find
  • 从root开始，小的走左右，大的走右边
• replace (to maintain the BST invariant)

找继任者的时候，如果删除元素没有子节点，只有左或右子节点，都很好办，但如果它有两个子节点，那么应该用哪个来接续呢？

原则仍然是要服从左边的比右边的小，所以你其实有两种选择：

• 把左边最大的数选出来 或
• 把右边最小的数选出来 因为它们的“来源”，肯定是能保证bst invariant的

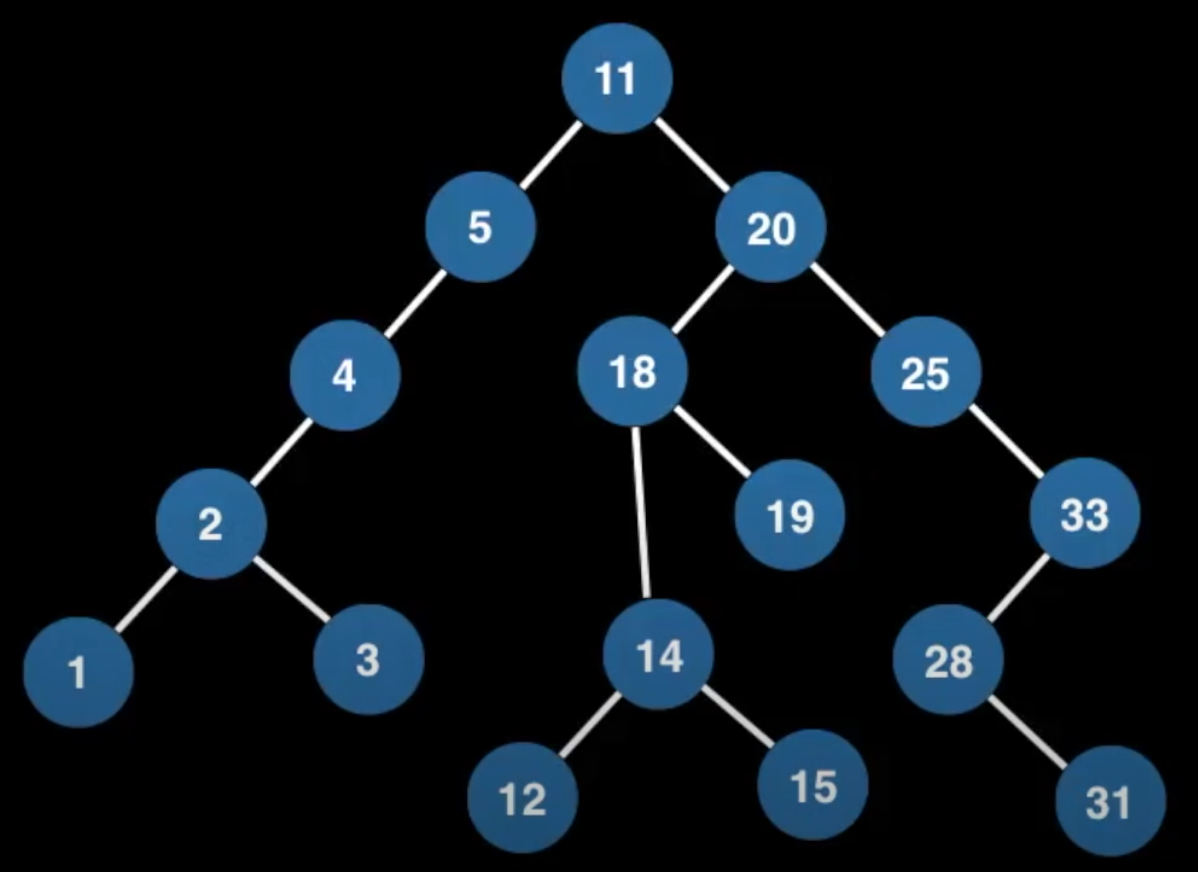
  * 这个数是要替换这个节点的，所以要比这个节点左边的数都大，及比右边所有的数都小，显然就是左边的最大数，或右边的最小数了。
  * 只是把找到的元素复制过去后，多了的那个怎么办呢？
  

• 递归 新找到的元素当然要从原来的位置删除，这时又根据它是否叶节点，单子节点还是全节点，来反复进行前面的操作，最终总是可以退出的

Tree Traversals

(Preorder, Inorder, Postorder & Level order)

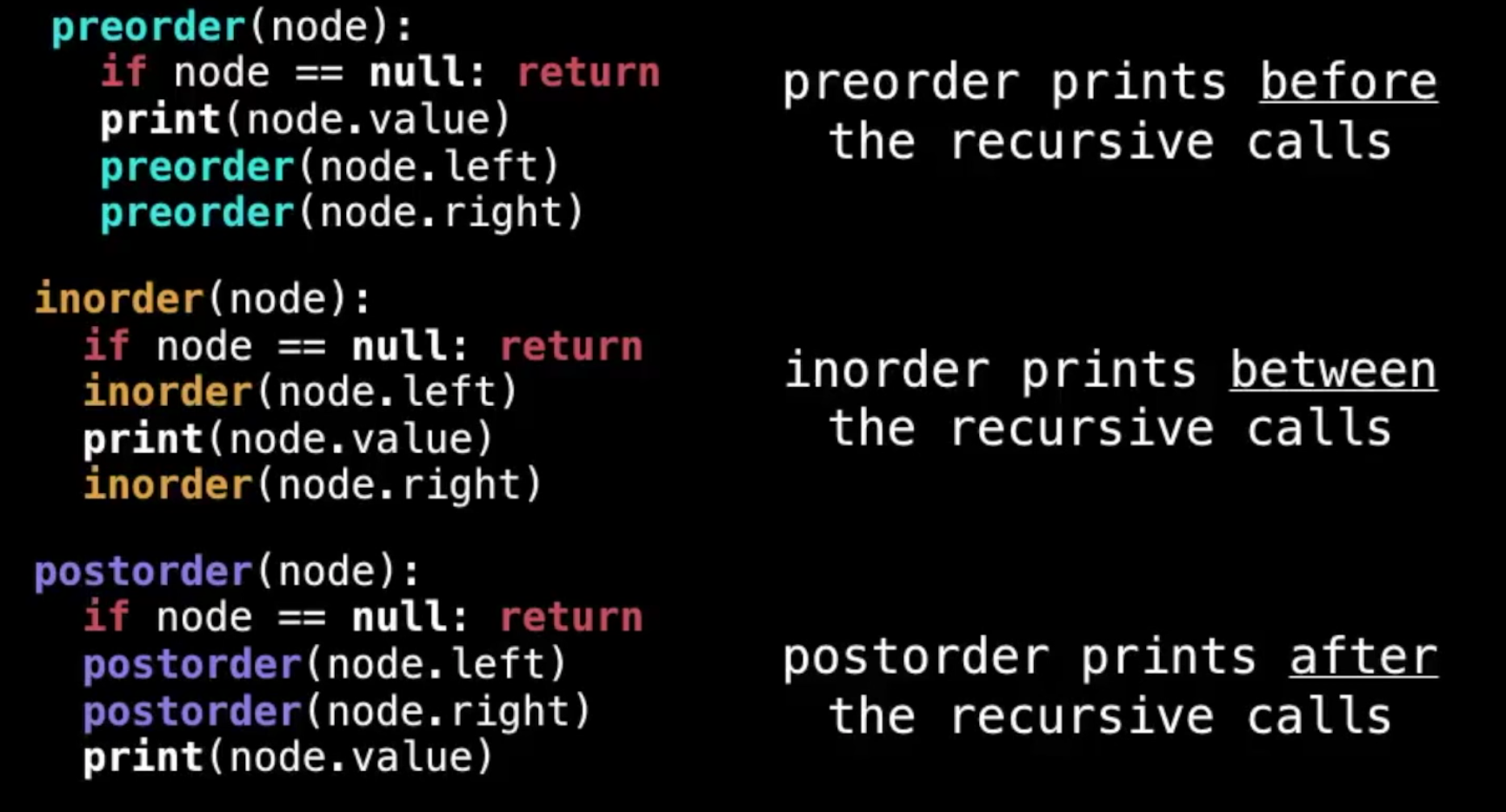
• preorder，在遍历左侧元素的时候，每次已经先取到元素了（最顶层）
• inorder里，遍历元素的时候，直到所有的left走完了，才取到第一个元素（最底层的）
• postorder里，也是遍历到最底层，但是下一步就是取兄弟节点了

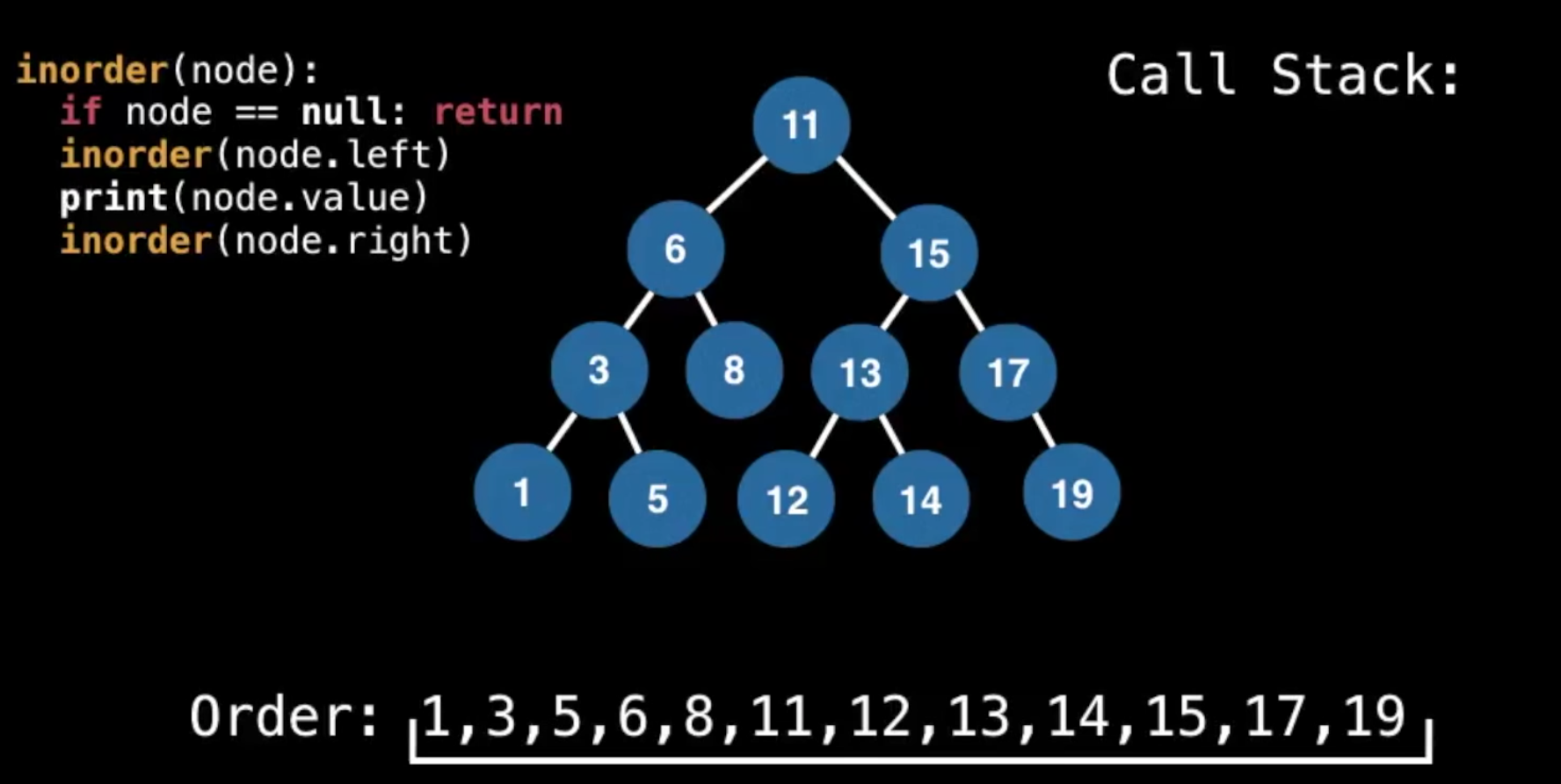inorder一个重要特征：它是从小到大排好序的！

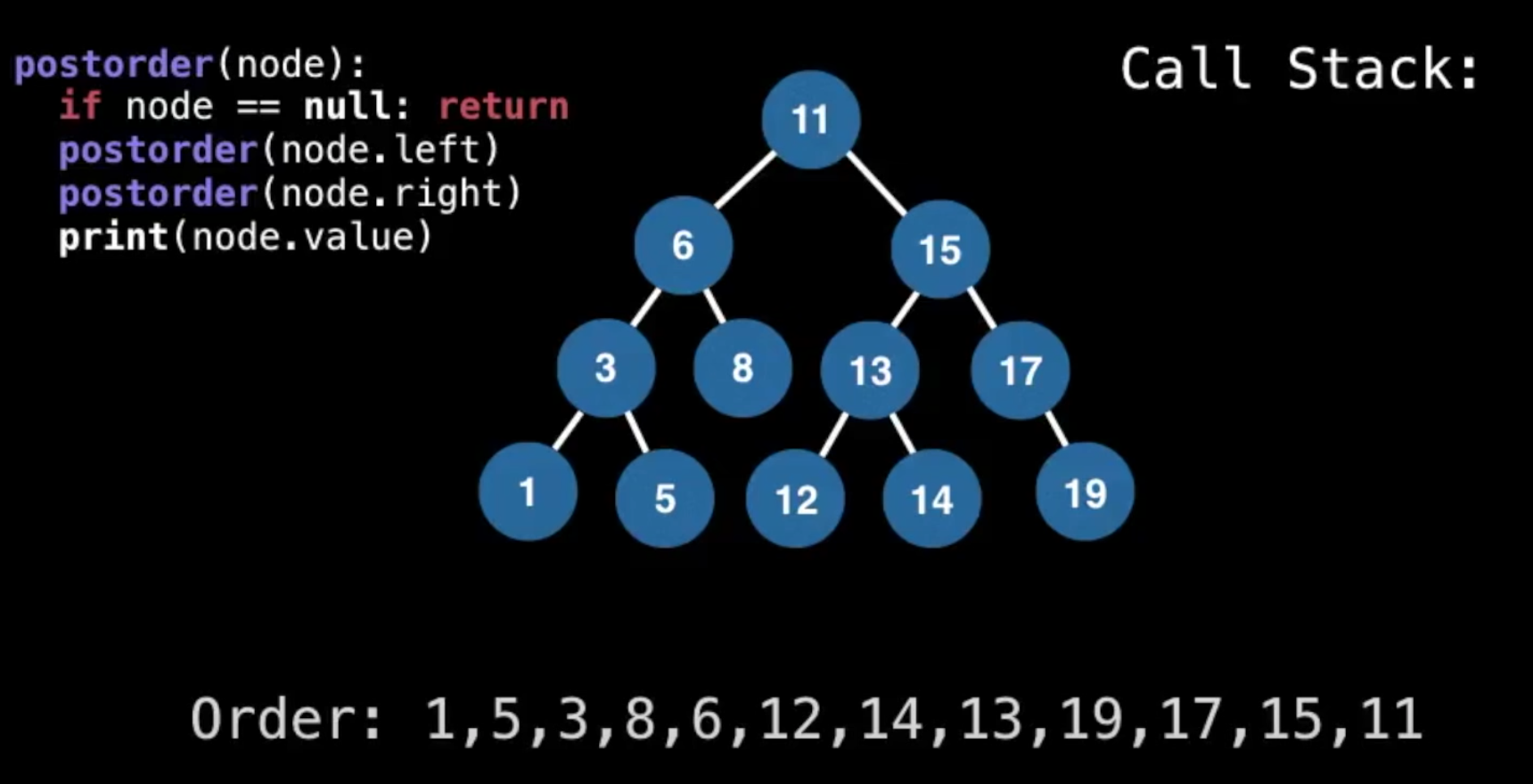preorder 和 postorder没什么特征，举一个post的例子观察下

而levelorder则是一层一层地取的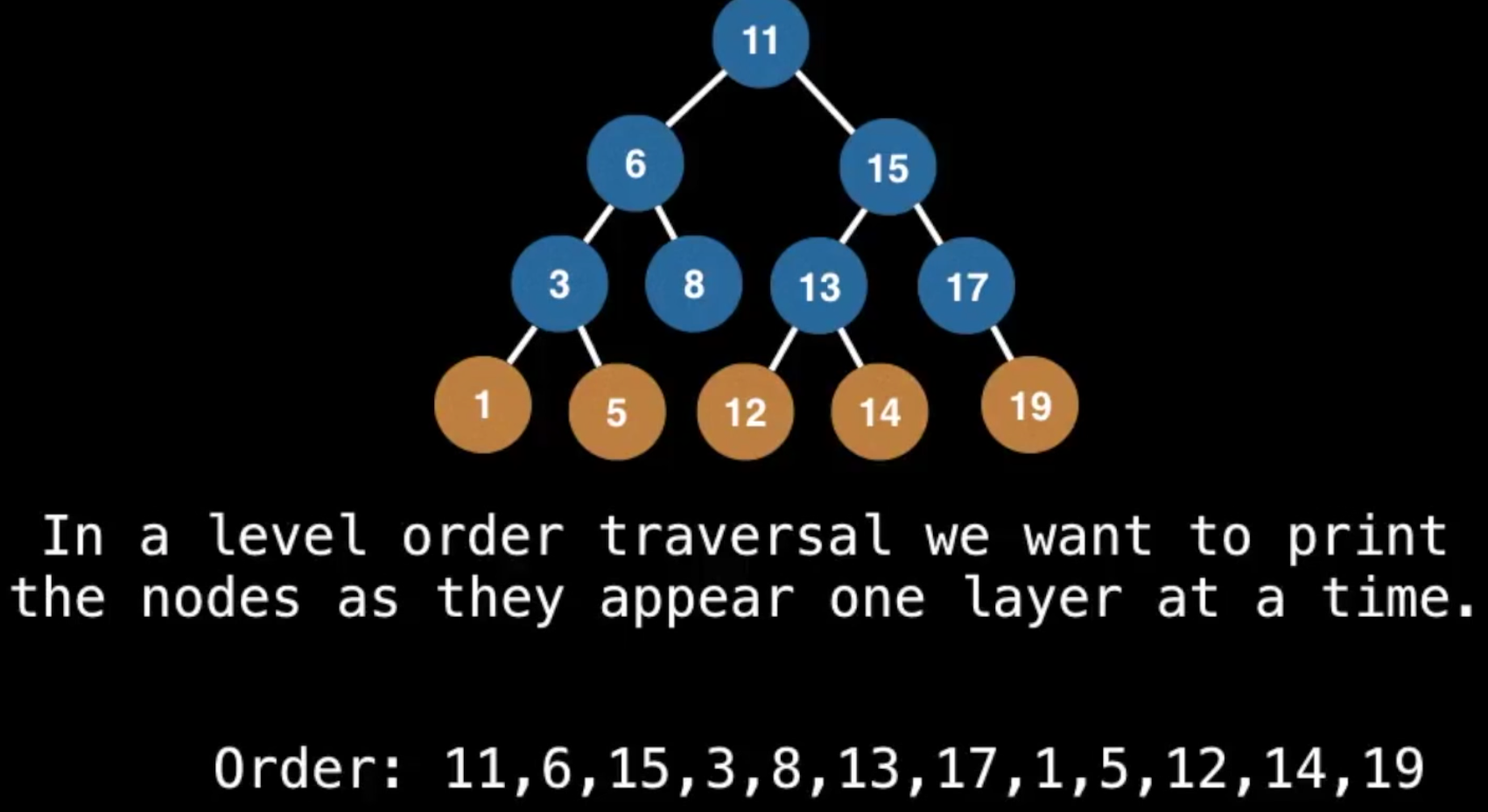： 这就是广度优先了（Breadth First Searth)BFS

实现BFS

1. 每处理一个parent的时候，把parent加到结果数组里
2. parent的子节点加到队列里
3. 每次从队列里取出一个值加到结果数组里（步骤1）
4. 该值的child加到队列里（步骤2）

其实就是步骤1，2的重复，比如：

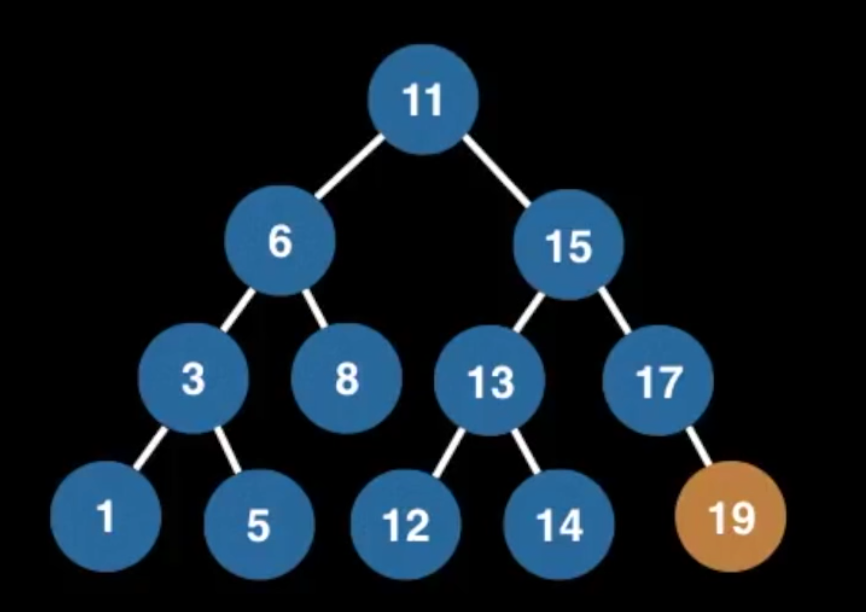
[11], [6, 15] 处理第1个数11， 队列里多了两个元素6， 15
[11, 6], [15, 3, 8] 从队列里取出6， 加入结果，它的子元素(3, 8)加入队列
[11, 6, 15], [3, 8, 13, 17]
[11, 6, 15, 3], [8, 13, 17, 1, 5]
[11, 6, 15, 3, 8], [13, 17, 1, 5] 这一步，8没有子节点了，队列变短了
[11, 6, 15, 3, 8, 13], [17, 1, 5, 12, 14]
[11, 6, 15, 3, 8, 13, 17], [1, 5, 12, 14, 19] 17只有一个child
[11, 6, 15, 3, 8, 13, 17, 1, 5, 12, 14, 19] 剩下的都没child了，全部拼进去

Hash Tables

• key-value pair
• using Hashing technique
• often used tracking item frequencies

what's hash function?

• maps a key x to a whole number in a fixed range.
  • e.g. $H(x) = (x^2 - 6x + 9)$ maps (0, 9)
  • 这个方程会为不同的x产生一样的y -> hash collision
• can hash arbitrary objects like string, list, tuple...
• must be deterministic(确定的x产生确定的y)
  • 因此key的应该是immutable的类型

关键词是range，你设计的function总要mod一下，将结果限制在一个范围内。这里你应该暂时能推测出hashtable的key可能就是数字吧？

hash collision

• separate chaining 用一种数据结构（通常是链表）保留所有冲突的值
• open addressing 为冲突的值选择一个offset（地址/值）保存 -> probing sequence P(x)

不管是怎么解决冲突，worst的情况下，hash table的操作时间也会由O(1)变成O(n)

怎么用HT来查找呢？不是把hash后的结果拼到原数据上，而是每次查询前，对key进行一次hash function，就能去查询了。

Open Addressing

probing sequences

• linear probing: P(x) = ax + b
• quadratic probing: p(x) = $ax^2 + bx + c$
• double hashing: p(k, x) = $x * H_2(k)$ 双重hash
• pseudo random number generator: p(k, x) = x * rng(H(k), x) 用H(k)(即hash value)做种的随机数

总之就是在这样一个序列里找下一个位置

假设一个table size 为N的HT，使用开放寻址的伪代码：

x = 1
keyHash = H(k)   # 直接计算出来的hash value
index = keyHash  # 偏移过后存在HT里的index

while table[index] != None:
    index = (keyHash + P(k, x)) % N  # 加上偏移，考虑size（N）
    x += 1 # 游标加1

# now can insert (k,v) at table[index]

Chaos with cycles

Linear Probling (LP)

LP中，如果你运气不好，产生的序列的下一个值永远是occupied的状态（一般是值域小于size），就进入死循环了。

假设p(x) = 3x, H(k) = 4, N = 9 那么H(k)+P(x) % N 只会产生{4,7,1}，如果这三个位置被占用，那就陷入了永远寻找下一个的无限循环中。

一般是限制probing function能返回刚好N个值。

当p(x)=ax的a与size的N互质，即没有公约数，GCD(a, N) = 1一般能产生刚好N个值。(Greatest Common Denominator)

注意，为了性能和效率的平衡，有load factor的存在，所以到了阈值，size就要加倍，N的变化，将会使得GCD(a, N) = 1的a的选择有变化，而且之前对N取模，现在取值也变发生变化，这时候需要重新map

重新map不再按元素当初添加的顺序，而是把现有HT里的值按索引顺序重新map一遍。比如第一个是k6, 即第6个添加进来的，但是现在第一个就重新计算它的值，填到新的HT里面去。

Quadratic Probing （QP）

QP 同样有chaos with cycles的问题，通用解决办法，三种：

1. p(x) = $x^2$, size选一个 prime number > 3, and $\alpha \leq \frac{1}{2}$
2. p(x) = $(x^2 + x) / 2$, keep the size a power of 2 （不需要是素数了）
3. p(x)= $(-1^x) \times x^2$, make size prime N $\equiv 3$ mod 4 ???

Double Hashing

Double Hashing: P(x) = $x \times H_2(k)$可见仍然类似一个一次的线性方程，$H_2(k)$就类似于ax中的a，设为$\delta$，相比固定的a, 这里只是变成了动态的，这样不同的key的待选序列就是不一样的（可以理解为系数不同了）

解决chaos:

1. size N to be a prime number
2. calculate: $\delta = H_2(k)$ mod N
   • $\delta=0$ 时offset就没了，所以需要人为改为1
   • $1 \leq \delta \lt N$ and GCD($\delta$, N) = 1

可见，虽然系数是“动态”的了，但是取值还是（1，N）中的一个而已，hash只是让其动起来的一个原因，而不是参与计算的值。

我们本来就是在求hash value，结果又要引入另一个hash function，显然这个$H_2$不能像外层这样复杂，一般是针对常见的key类型(string, int...-> fundamental data type)的universal hash functions

因为N要是一个素数，所以在double size的时候，还要继续往上找直到找到一个素数为止，比如N=7, double后，N=14，那么最终，N=17

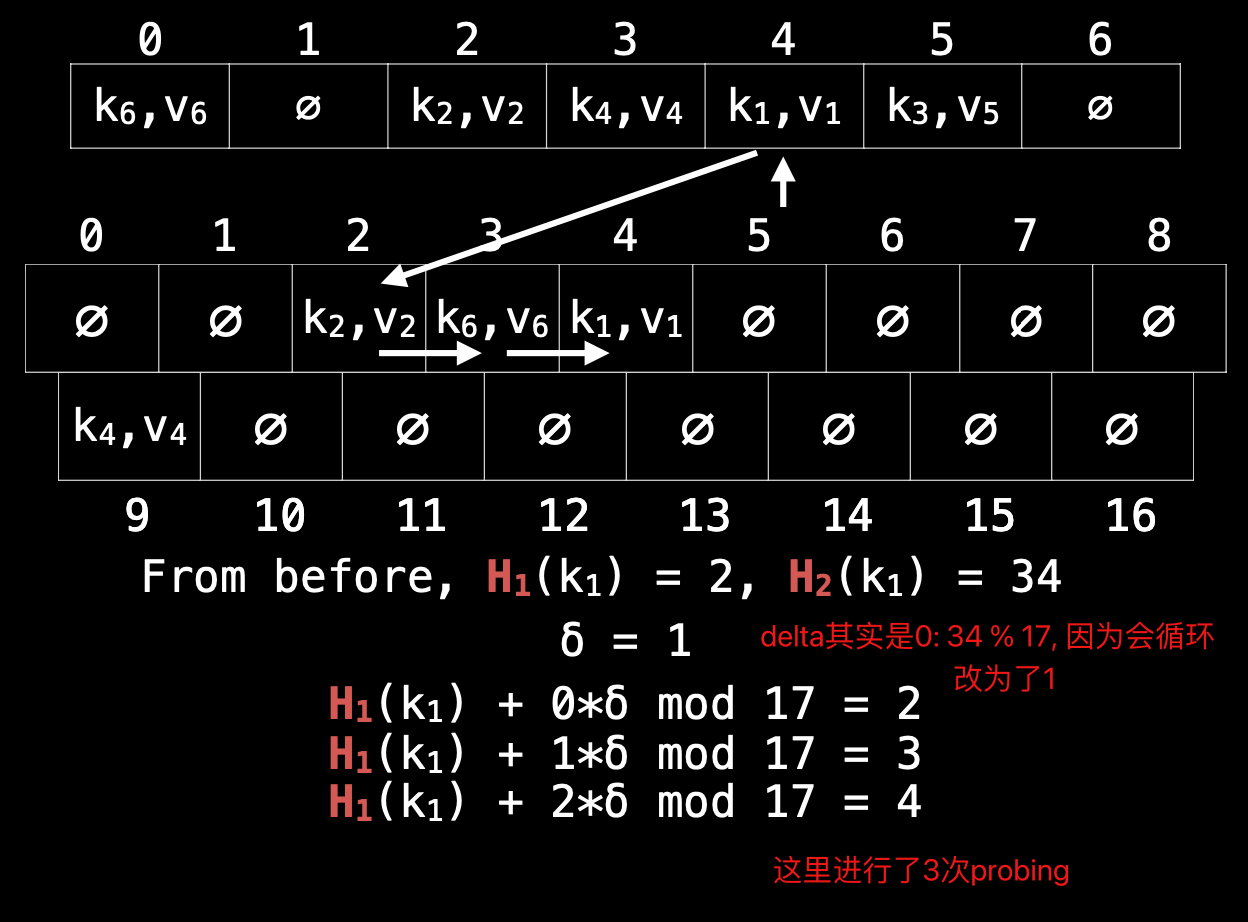
Issues with removing

因为冲突的hash value需要probing，probing的依据是从序列里依次取出下一个位置，检查这个位置有没有被占用，那么问题就来了，如果一个本被占用的位置，因为元素需要删除，反而变成没有占用了，这有点类似删除树节点，不但要考虑删除，还要考虑这个位置怎么接续。

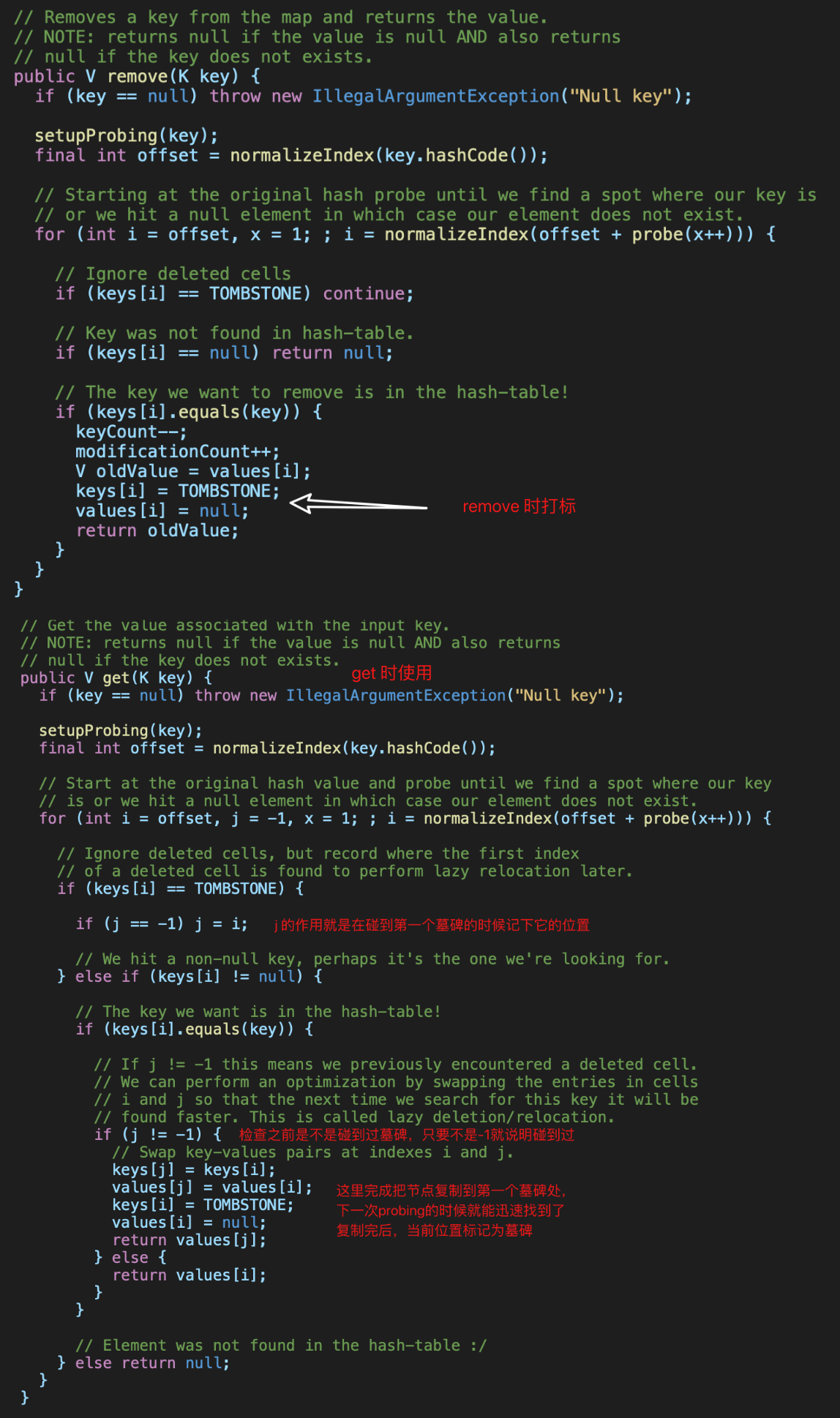
lazy deletion 但HT机制比树要复杂，为了避免反复应用probing函数重新摆放后续所有节点，干脆就在删除的位置放置一个预设的标识，我们称为墓碑(tombstone)，而不是直接置空，然后所有的查找和添加加上这一条规则，就能快速删除又无需重新排序。

大量删除会造成空间浪费，但无需立即处理：

1. 添加元素允许添加到墓碑位置
2. 到达阈值容量需要倍增的时候有一次重排，这个时候就可以移除所有的墓碑

如果查找一个hash value，连续3个都是墓碑，第4个才是它，这是不是有点浪费时间？确实，所以还可以优化，当你查找过一次之后，就可以把它移到第一个墓碑的位置，这样，下次查询的时候速度就会快很多了。

整个机制，叫lazy deletion

Fenwick Tree (Binary Indexed Tree)

树状数组

Motivation

• 计算数组里任意连续片段的和，最直观的方案当然是累加O(n)
• 但是如果你有一个记录了每个节点到当前位置时的累加和的数组（prefix sum），立刻变成了常量时间
• 问题更新数据变成了线性时间（后续所有的求和都要改一变）
  • great for static arrays

所以： Fenwick Tree is an efficient data structure for performing range/point queries/updates.(即在上面的动机上，还考虑了update的效率)

前面的例子在update时效率不高，所以Fenwick Tree用了一种聪明的方式，不是累加所有的值，而是分段累加，具体实现看下图：

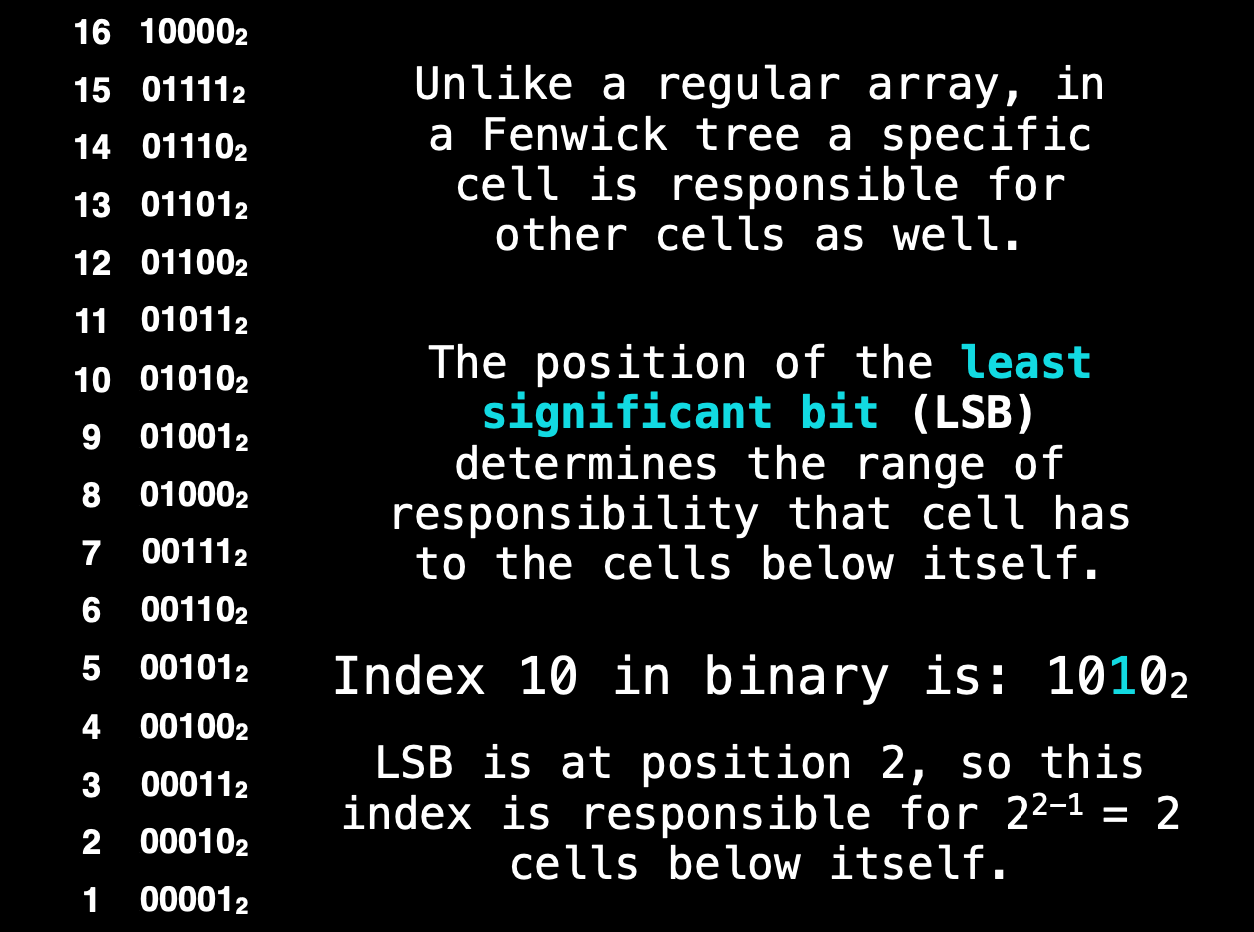
• 把索引值用二进制表示
• LSB的解释看图，实际应用上，就是看从低位到高位第一个1的右边有几个0，假设为n个
• 那么该cell上存的值就是前$2^n$个cell的值的和

例子是索引10， 二进制是1010， 最右边有2个零，那么它保存它4个位置的和。 也就是说，如果你要求和，如果用了cell 10位置的值的话，至少可以省掉3次累加。

当然，它还有更牛逼的特性，结合range query一起来看吧： 蓝线表示的是当然位置上累加了前几个位置的值，已经很有规律了

假如计算前11个值的和，过程是：

1. 11的索引是1011，右边没有0，所以当前的和为A[11]
2. 根据$2^0$来移位，来到10。
   • 右边一个0，所以它管$2^1$个presum，目前A[11] + A[10]
   • 下一个索引自然要减2了，来到8
3. 8是1000，3个零，所以它存了$2^3=8$个值的和，那就是全部了

所以：sum = A[11] + A[10] + A[8]

• 心算sum(0,7)巩固一下
• 用sum(11,15)演示子区间，其实就是多减1次，至于是减到10还是减到11，看描述，比如这里11是要参与计算的，那就是把前10个减掉就行了。

上面演示的都是worst的情况，即首位为1，除了这种情况，别的位都至少存了前$2^n$个元素的值（比如16，直接得到16个元素的和）

这里都没讲你是怎么做这个tree的，而是怎么使用它。先弄清楚使用场景再谈构建。

Point Update

复习一下LSB，虽然可以直接数最右边的零的个数，但数学其实是：

• 13 = 1101 ($2^3 + 2^2 + 2^0 \Rarr 10^3 + 10^2 + 10^0 $)
• 减去最右边的1和0 => 1100 （$2^3+2^2=12$) 所以下一个数是12
• 减去最右边的1和0 => 1000 就是8了
• 再减就是0了 而按$2^n$来计算个数的话就是这样的：
• 13 = 1101, 没有0，就是移1位，变成12
• 12 = 1100， 2个0， 就是移4位，变成8
• 8 = 1000， 3个0， 移8位，变成0

现在来讲update，前面知道，update会级联影响到所以把该cell考虑进去的节点，因此，它需要反着往上找（极端情况当然是找到最后一个元素，通常这个元素就是整个数组的值，所以任何元素的更改，肯定都会影响到它）

前面找下一个节点用的是减法，现在就要用加法了，比如我更新了cell 9, 用以上两种任意一种方法来计算：

• $9 = 2^3 + 1 \Rarr 10^3 + 1 = 1001, +1 = 1010 = 10$
• 1010 + 10 = 1100 = 12
• 1100 + 100 = 10000 = 16 到顶了， 所以需要把9, 10, 12, 16分别应用这个point的更新，也就是说只有这几个cell把9计算进去了。

当然，可以看一下左边的示意图，更直观

function add(i, x): 
    while i < N:
        tree[i] = tree[i] + x 
        i = i + LSB(i)

代码非常简单，就是不断通过LSB找下一个位置去更新就行了。

Construction

现在来讲构建

function construct(values): N := length(values)
    # Clone the values array since we’re # doing in place operations
    tree = deepCopy(values)
    for i = 1,2,3, ... N:
        j := i + LSB(i)
        if j < N:
            tree[j] = tree[j] + tree[i]
    return tree

几乎就一句话，就是把元素按原数据摆好（即不加别的节点）后，每次找到当前元素影响的上一级（不再向上冒泡）

• 比如1，把1算进去的有2，虽然上面还有4， 8， 16，但只把1更新到2
• 到2的上一级是4 (2 + lsb(2) = 4), 把节点2的现值（已经加了节点1）加到4去
• 所以核心算法始终只有两个变量，i，j代表最近的包含关系

一些算法换成位运算

• lsb(i): i & -i
• i -= lsb(i) => i &= ~lsb(i)

Suffix Array

• 字符串的所有子字符串后缀组成数组
• 对子串根据首字母进行排序
• 排序后原有的index就被打乱了
• 这个乱序的indices就是Suffix Array

做尾缀子串的时候通常是从个字母开始越找越多，这就有了一个原生顺序，然后用首字母排序后，这个顺序就被打乱了

提供了一种compressd representation of sorted suffixes而无需真的把这些子串存起来。

• A space efficient alternative to a suffix tree
  • a compressd version of a trie?

能做所有suffix tree能做的事，并加添加了Longest Common Prefix(LCP) array

Longest Common Prefix (LCP) array

继续上面的Suffix Array，字母排序后，我们一个个地用每一个元素同上一个元素比，标记相同前缀的字母个数，这个数字序列就是LCP

比如adc, adfgadc, 前缀ab是相同的，那就是2。

第一个元素没有“上一个”去比，所以LCP数组第1位永远是0？（是的，其实是undefined，但一般设0）

衡量的是相邻的suffix array元素的前缀间有多少个字母相同。

当前也可以和下一个元素比（这样最后一个元素的LCP肯定是0了，原理同上）

Find unique substrings

找到（或计数）一个数组的所有（不重复的）子元素。可以逐个substring遍历，$O(n^2)$，下面看看更快也更省空间的LCP方案。

找“AZAZA”的不重复子串: A,AZ,AZA,AZAZ,AZAZA,Z,ZA,ZAZ,ZAZA,A,AZ,AZA,Z,AZ,A，把重复的标注了出来。 LCP是这样的： LCP|Sorted Suffixes| -|- 0|A 1|AZA 3|AZAZA 0|ZA 2|ZAZA

我们知道第一列指的是“重复个数”，也就是说，如果按我们手写的那样去遍历，至少有这么多重复的子串，重复的既是“个数”，也是“组合方式”。

所以如果我们只需要计数的话，把右边的数出来就知道有会有多少个重复的了，此例为6.

$\tt unique\ count = \underbrace{\frac{n(n+1)}{2}}_{substr\ count} - \underbrace{\sum_{i=1}^n LCP[i]}_{duplicates}$

这是LCP的应用之一，利用了LCP本身就是在数重复次数的特征。

K common substring problem

n个字符串，找出一个子串，它至少是k个字符串的子串，求最大子串。$2\leq k \leq n$

即如果有k=2，那么这个子串只需要是其中两个的子串就行了，如果k=n，那么就需要是每一个字符串的子串。

直接上图

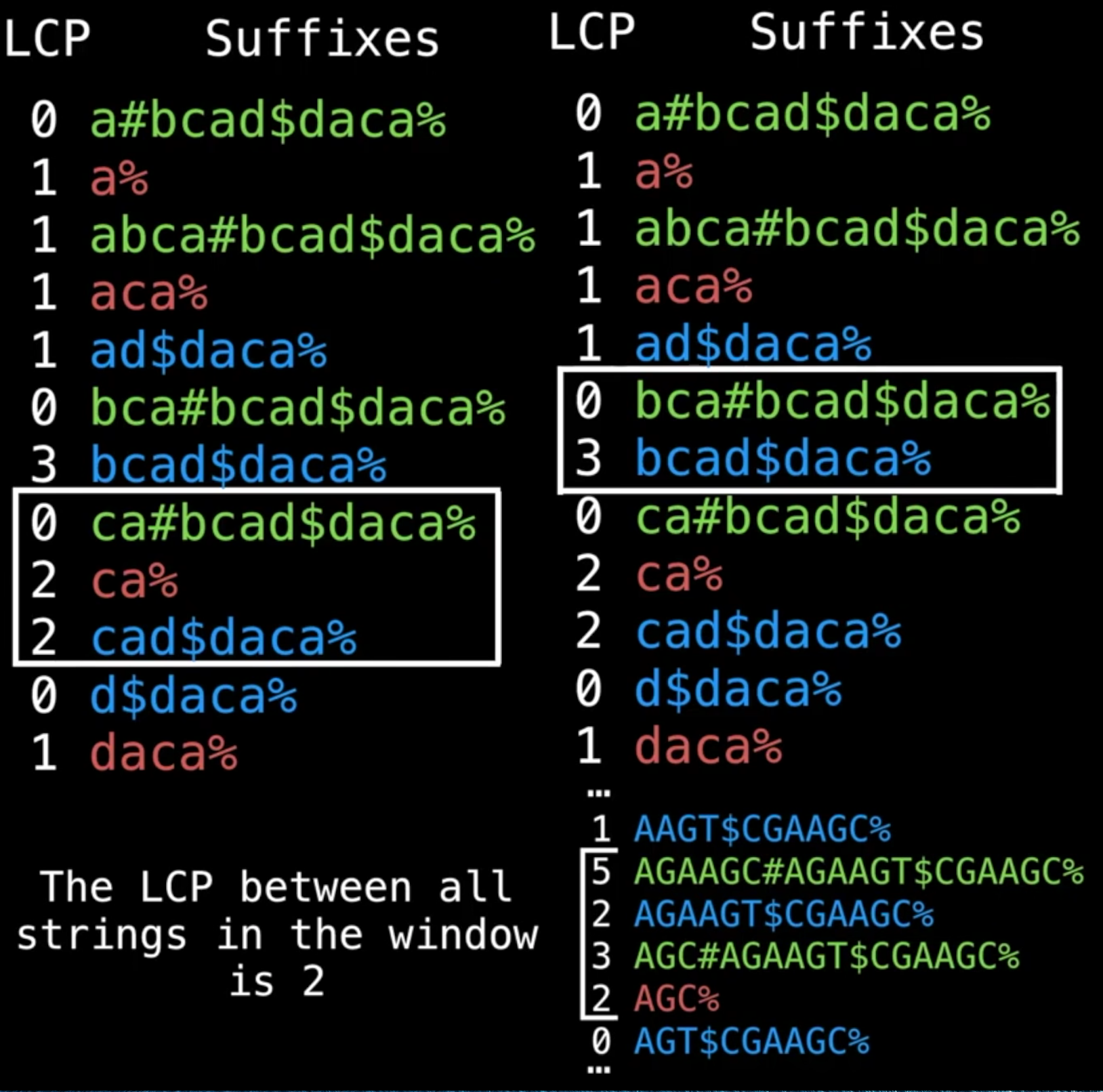
• 图1演示k=3时，找到了ca，即3个串里都有的是ca
• 图2演示k=2时，找到了bca，即bca存在2个串里
• 图3演示的是用了size=4的滑窗才包含了3个字符串，以及最大匹配是AG

步骤：

1. 首先，用几个分隔符把字符串拼接起来
   • 分隔符字符串里不会出现
   • 分隔符的排序要小于所有字符
2. 图中染色的依据是prefix是哪个串里的就染成什么颜色
3. 开始滑窗比较
   • 滑窗必须要能包含k种颜色
   • 所以滑窗大小不是固定的，有时候相邻几个都是来自同一个字符串
   • 滑窗里除0外的最小值，就是符合条件的最大共同长度，如图3，最大匹配长度是2
   • 课程里动画演示滑窗其实不是用滑的，而是用的爬行
     • 即下界往下，包含了所有颜色之后，上界也往下，这样蠕行前进，每一步判断滑窗里的内容
4. 额外需要一个hash table来保存切片与颜色的映射关系。
   • 如果是例子这么简单，我可以直接检查第一个出现的分隔符，是#就是绿色，出现$就是蓝色，%就是红色

核心就是：

• 取子串是从后向前取的
• 但比较是从前向后比的
• 前面的元素可能来自任何一个子串（只要足够长）
• 从前面排序，客观上就把来自不同字符串的相同字母打头的子串给排到一起了

这就是为什么在Suffix Array的内容里面出现Longest Common Prefix的内容的原因了.

聪明。

Longest Repeated Substring (LRS)

这个比暴力遍历要简单太多，直接找LCP最大值即可

Balanced Binary Search Trees (BBST)

• 满足low (logarithmic) height for fast insertions and deletions
• clever usage of a tree invairant and tree rotation

AVL Tree

一种BBST，满足O(log n)的插入删除和查找复杂度，也是第一种BBST，后续出现的更多的：2-3 tree, AA tree, scapegoat tree, red-black tree(avl的最主要竞争对手)

能保持平衡的因子：Balance Factor (BF)

• BF(node) = H(node.right) - H(node.left)
• H(x) = height of node = # of edges between (x, furthest leaf)
• 平衡就是左右平均分隔，所以要么均分，要么某一边多一个，BF其实就是(-1, 0, 1)里的一个了 <- avl tree invariant

一个node需要存：

• 本身的(comparable) value
• balance factor
• the height of this node
• left/right pointer

使树保持左右平衡主要是靠rotation，极简情况下（三个node），我们有两种基本情况（left-left, right-right），有其它情况就旋转一次变成这两种情况之一：

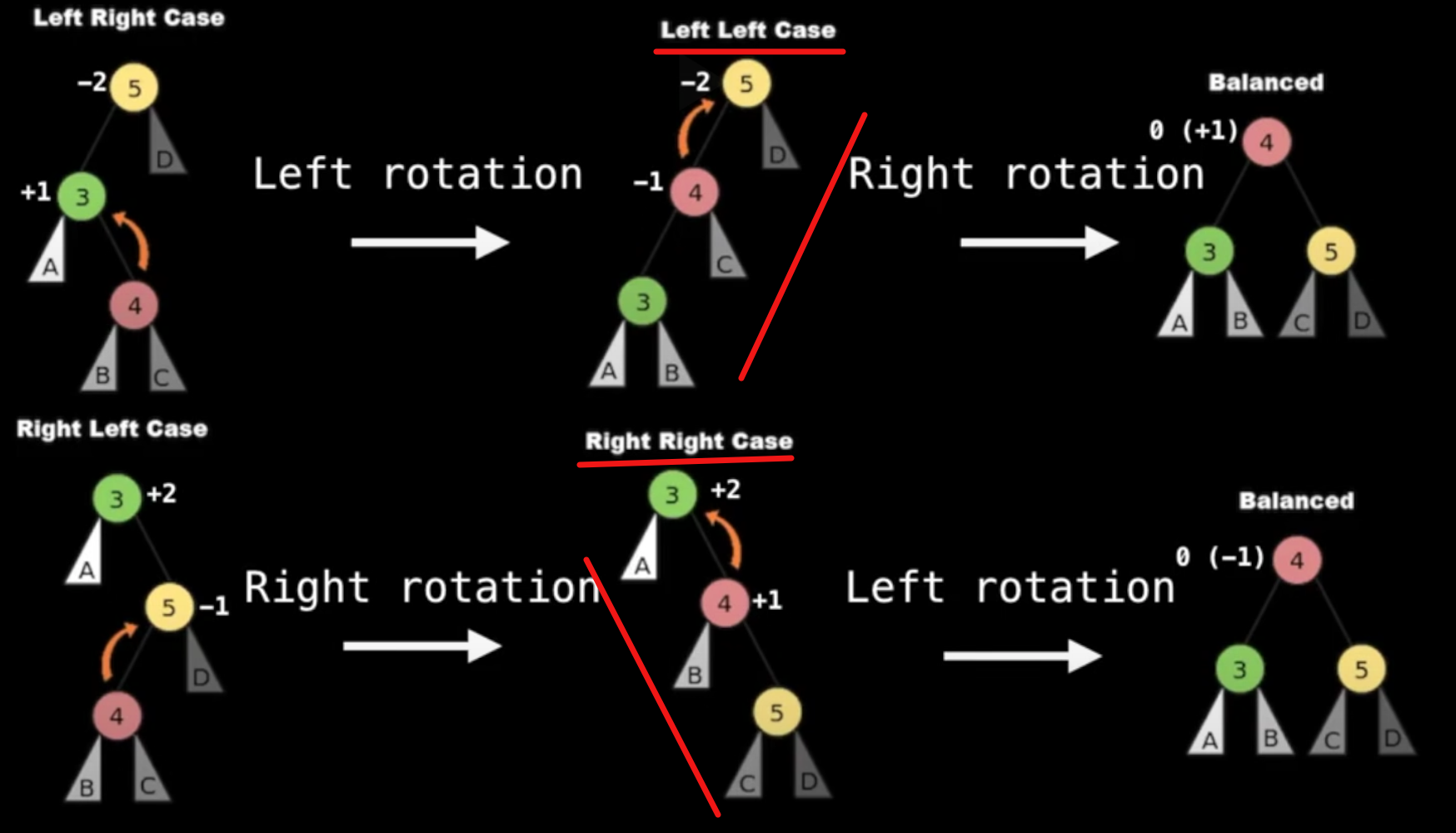
Insertion

一次插入需要考虑的是，插在哪边，以及插入后对bf, height和balance的破坏

其中修复平衡就是上图中几个基本结构的转换

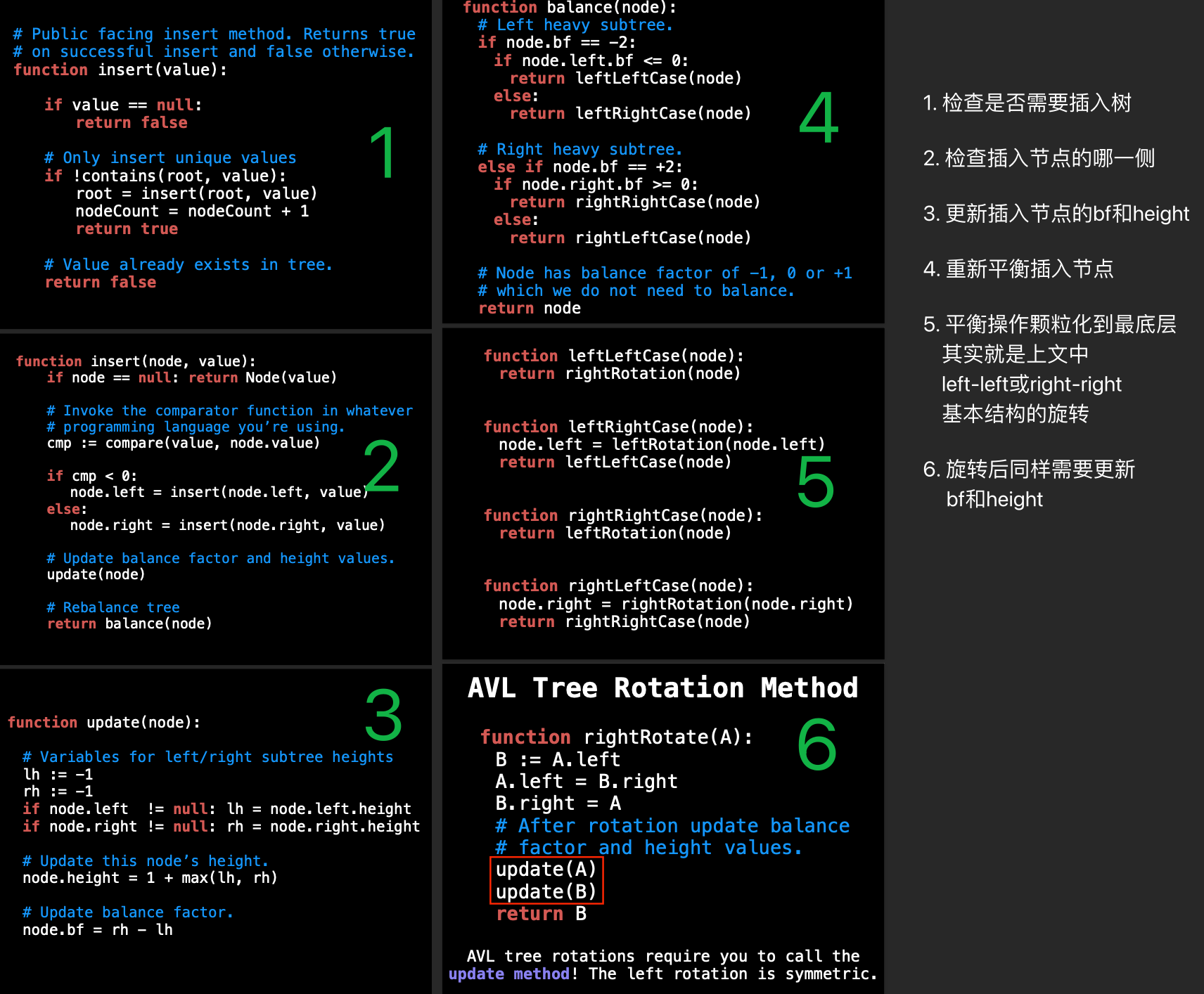
Removial

avl树就是一棵BST，删除节点分两步：

1. 按照bst的方法查找节点，即小的在左边找，大的在右边找
2. 也按bst的原则删除元素，即找到元素后，把左边的最大值或右边的最小值拿过来补上删除的位置
3. 这一步是多出来的，显然是要更新一下节点的bf和height，及重新balance一次了。

前两部分参考BST一章，流程伪代码：

function remove(node, value): ...
    # Code for BST item removal here
    ...
    # Update balance factor
    update(node)
    # Rebalance tree
    return balance(node)

Indexed Priority Queue

• a traditional priority queue variant
• top node supports quick update and deletions of key-value paris

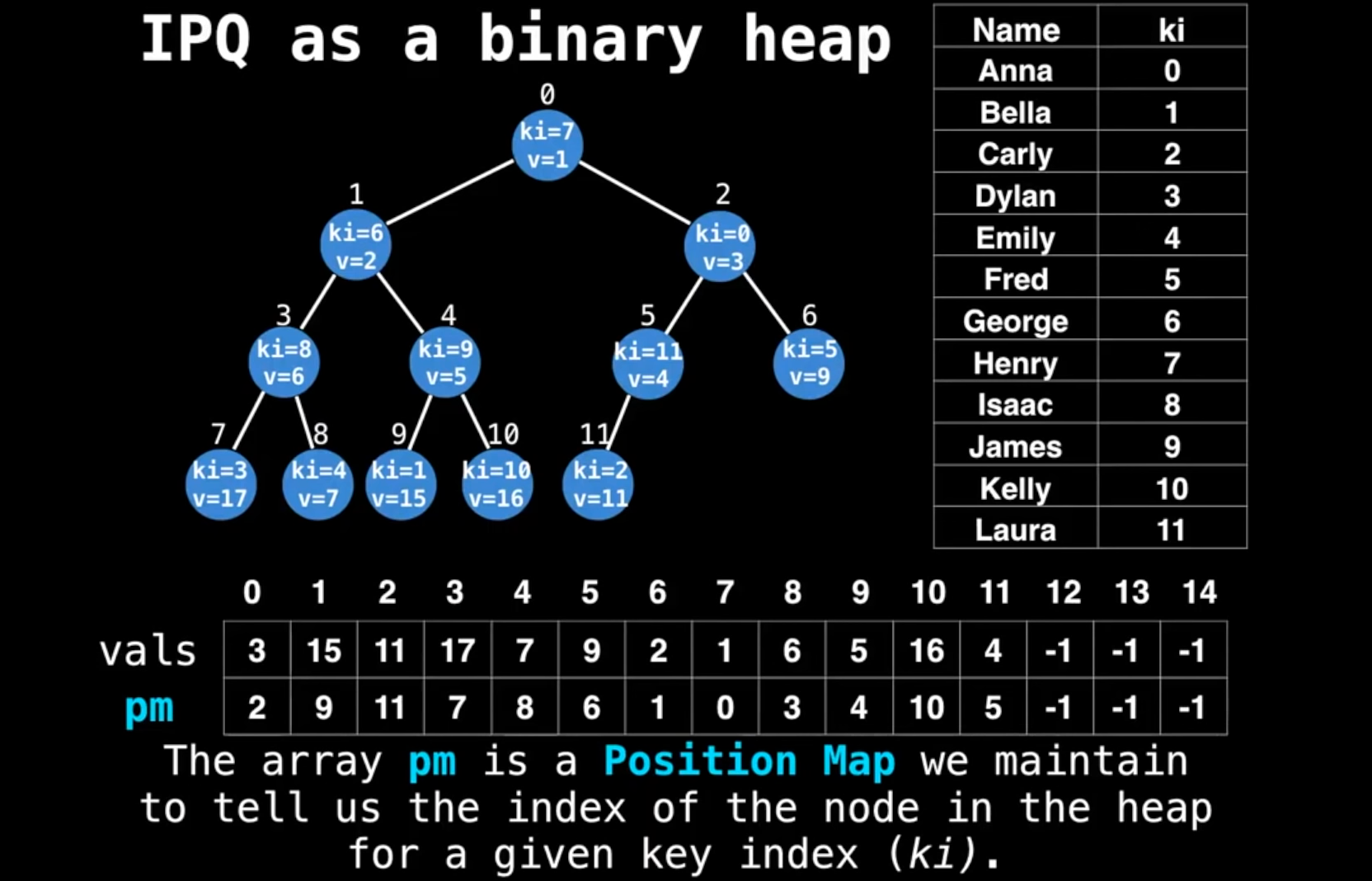观察这个图，数据是Anna, Bella...等等，

• 首先，为这一堆数据进行任意排序，得到一堆索引(0,1,...)
• 然后组一个binary heap，这样每个元素又获得一个索引，就是在heap上的序号（Position Map）

通过两组索引迅速找到key（就是人名）在堆中的位置，比如：

• George，ki = 6, pm = 1
• kelly, ki = 10, pm = 10
• ...

现在能迅速找到数据源在堆上的位置了，那么如果反过来呢？比如堆上索引3是数据源的谁？

• pm = 3 -> ki = 8 -> Issac BINGO!!!

但神奇的事发生了，有人希望复用ki这个自然数序列（闲的蛋疼？），于是多做了一个数组，把ki定义为heap上的索引，与元素原来的ki进行映射（Inverse Map）:IM

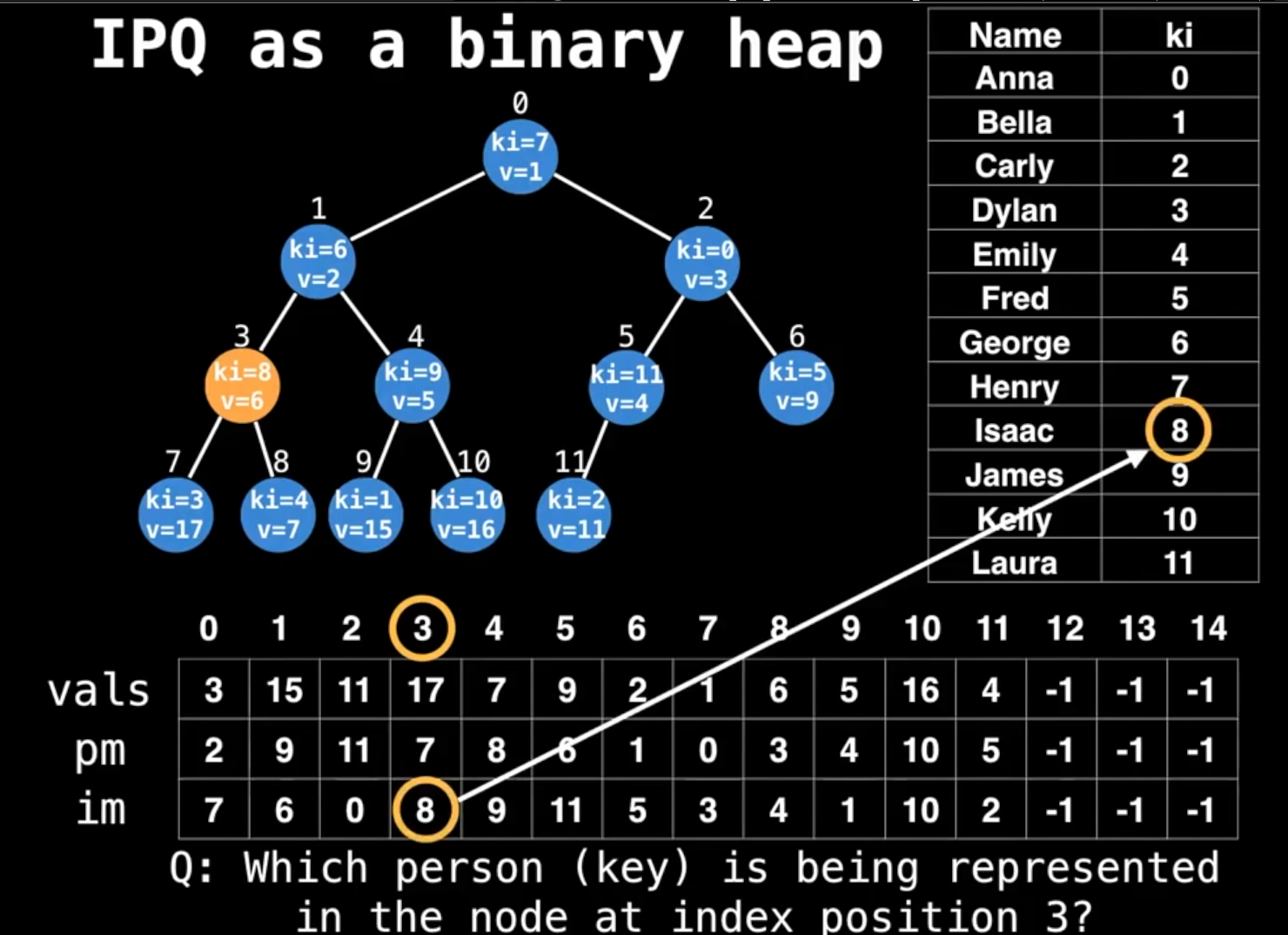可以看到，这张图上张个ki到im的映射，与pm到ki的映射其实是一样的，也就是说重定义了一下，并没有引入新的东西。

这个时候，我们直接用ki的3就能找到im的8，继而找到数据源的Issac了。

Insertion

上面的数组，我们往里面添加第12条数据试试:

• {ki:12, pm: 12, im:12, value:2}
• 显然违反了binary heap的 invariant，向上冒泡，也就是跟{ki:12, pm:5, im:2, value:4}的节点互换
• 此时，数据源肯定不会变，但是节点变了，pm的值就要交换（5， 12 互换）
• pm变了，把pm当成ki的映射表im也要变（12， 11互换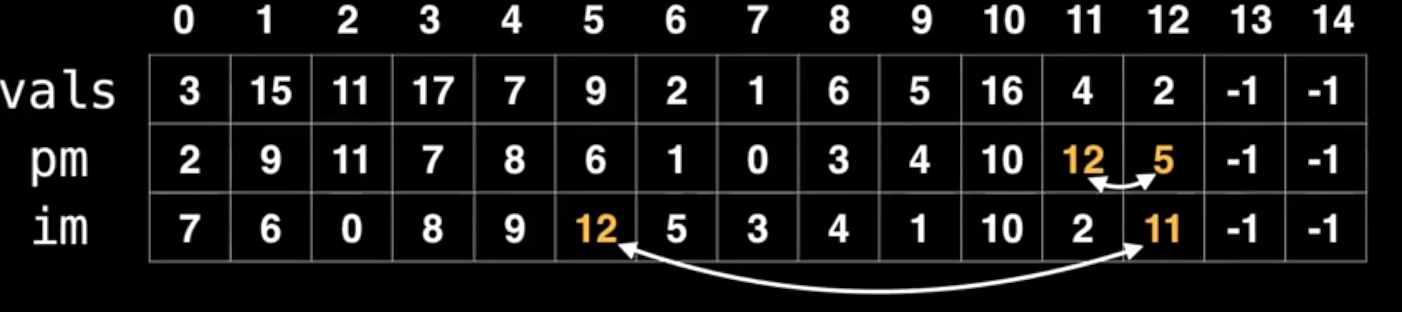） 仔细观察图片，搞清楚第一行ki在两次互换时的身份就明白了
• pm的互换是直观的，就是节点的位置
• 知道pm互换的依据后（2，5），在第一行找2，5对应的im值互换，因为在这个映射里，相当于pm与原ki的映射，pm此时是（2，5）了。

同样逻辑继续冒泡就是了。

pseudo code:

# Inserts a value into the min indexed binary 
# heap. The key index must not already be in 
# the heap and the value must not be null. 
function insert(ki, value):
    values[ki] = value
    # ‘sz’ is the current size of the heap
    pm[ki] = sz  # 对应上图，意思就第一行索引器是ki
    im[sz] = ki  # 对应上图，意思就是一行索引器是pm
    swim(sz)     # 这里传进去的pm，即heap上节点的索引
    sz = sz + 1  # 添加成功，size加1

理论上，添加元素到最后一个, sz和ki应该是相等的（因为都是尾巴上）

# Swims up node i (zero based) until heap 
# invariant is satisfied.
function swim(i):
    # 比父节点小就冒泡，注意入参i是节点上的索引，即pm
    for (p = (i-1)/2; i > 0 and less(i, p)): 
        swap(i, p)  # 所以这里传的也是pm
        i=p
        p = (i-1)/2

function swap(i, j): 
    # 我们交换了节点，需要交换pm表里的值，和im表里的值
    # 交换pm的值需要数据源的索引，即ki，而ki能从im表里用pm算出来
    # 所以ki = im[pm] 这里i,j是pm，所以im[i]自然就是i对应ki
    # pm[ki]当然就是pm[im[i]]了：
    pm[im[j]], pm[im[i]] = j, i
    im[i], im[j] = im[j], im[i]

function less(i, j):
    return values[im[i]] < values[im[j]]

还是那句话，理解清楚那三行映射表里第一行的动态含义，就不会有问题。

• pm表要key index来索引
• im表要node index来索引 在操作时，只需要知道传入的是哪种索引，及时转化就行了。

有了索引，lookup的时间复杂度就是常量时间了：O(1)

Polling and Removals

没有什么特殊的,仍然是找到节点,与最后一个交换,移除最后一个节点,然后再看最后一个在堆里是上升还是下降. 仍然是记得每一步交换,相应的几个索引值也需要随之交换.(polling 其实就是移除第1个节点,本质上还是 removal)

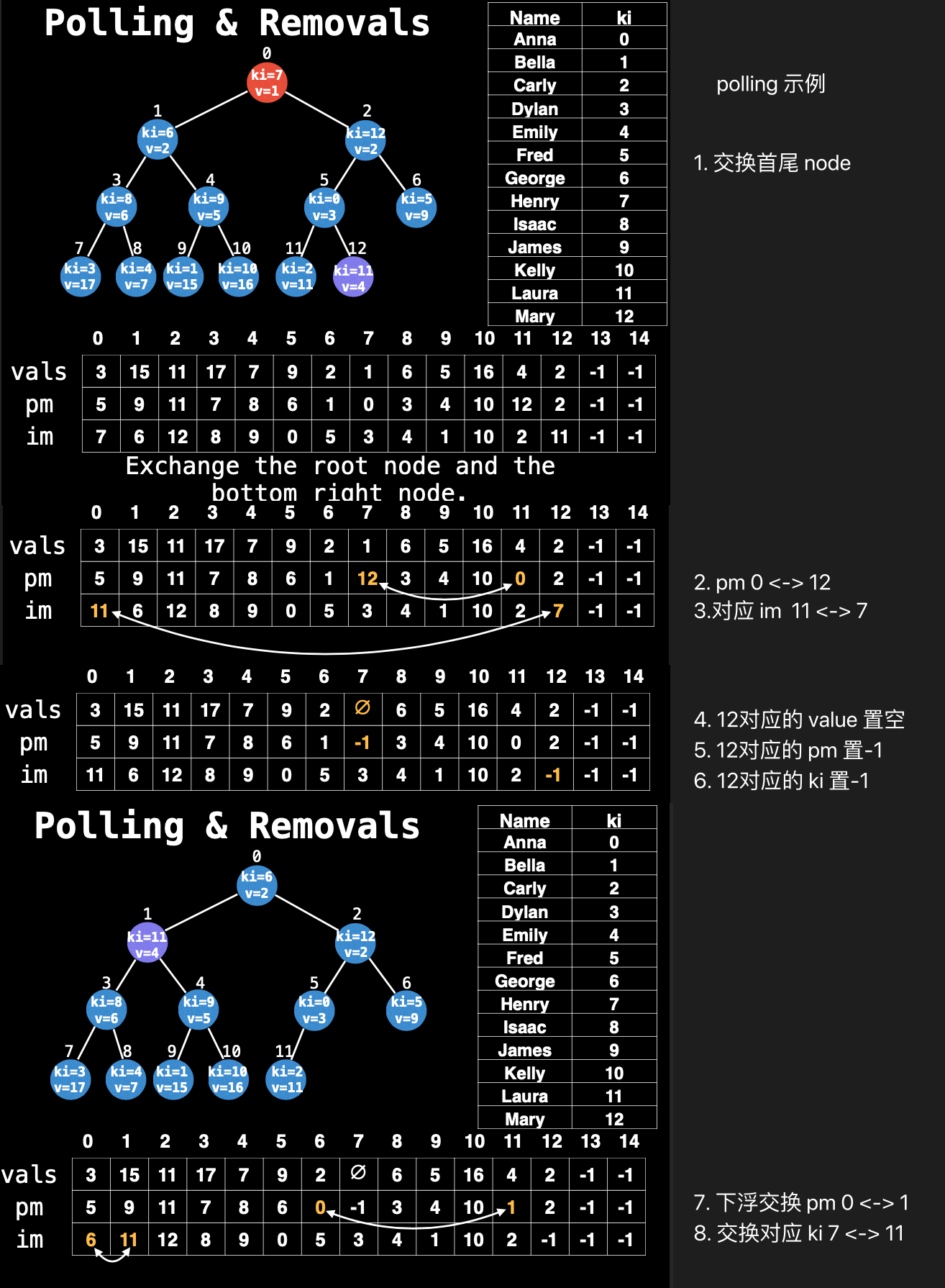
pseudo code

# Deletes the node with the key index ki
# in the heap. The key index ki must exist 
# and be present in the heap.
function remove(ki):
    # 注意，这里送进来的是ki，而不是node index(pm)
    # 说明业务需求一般是操作数据源，而不是操作堆
    i = pm[ki]    # 转成节点索引
    sz = sz - 1   # 与最后一个元素交换，用size来做节点索引
    
    # 下面三个子函数送入的就是节点索引了
    swap(i, sz) 
    sink(i)
    swim(i)

    values[ki] = null  # 数据源对应的值置空，所以用ki
    pm[ki] = -1        # 数据源对应的节点置空，所以用ki
    im[sz] = -1        # 反查表用节点索引，此处size就是最后一个节点的索引

sink pseudo code

# Sinks the node at index i by swapping 
# itself with the smallest of the left 
# or the right child node.
function sink(i):
    # 这是堆操作,传入的索引也是节点索引,没问题
    # sink是下沉，但不是跟BTS一样找左侧最大右则最小那种直接换
    # 而是一层层往下换
    # 即一次while只跟左右子级比大小，确实比子级还小的话，就替换，然后再跟下一层比较
    while true:
        # 利用二叉树特性算出子节点
        # 默认左边最小，然后再看右边是不是更小
        left =2*i+1
        right = 2*i + 2
        smallest = left
    # 右边不越界，且小于左边，就设右边
    if right < sz and less(right, left):
        smallest = right
    # 左侧都越界了，或已经比最小值大了，说明不需要下沉了
    if left >= sz or less(i, smallest):
        break
    # 只要没有break，说明能交换，然后把交换后的作为下一个循环的起点
    swap(smallest, i)
    i = smallest

Updates

更新节点要简单的多:

• 用ki找到value，把值更新
• 然后根据新value实际情况上浮或下沉

# Updates the value of a key in the binary 
# heap. The key index must exist and the
# value must not be null.
function update(ki, value):
    i = pm[ki]
    values[ki] = value
    sink(i)
    swim(i)

Decrease and Increase key

不好说，先看代码吧：

# For both these functions assume ki and value 
# are valid inputs and we are dealing with a
# min indexed binary heap.
function decreaseKey(ki, value):
    if less(value, values[ki]): 
        values[ki] = value 
        swim(pm[ki])
        
function increaseKey(ki, value): 
    if less(values[ki], value):
        values[ki] = value 
        sink(pm[ki])

代码里是跟一个固定值比较，只要ki对应的值比它大(desreaseKey)或小(increaseKey），就用这个固定值来替换它，并且在value改变后根据实际情况上浮或下沉。