RNN梯度消失与梯度爆炸推导
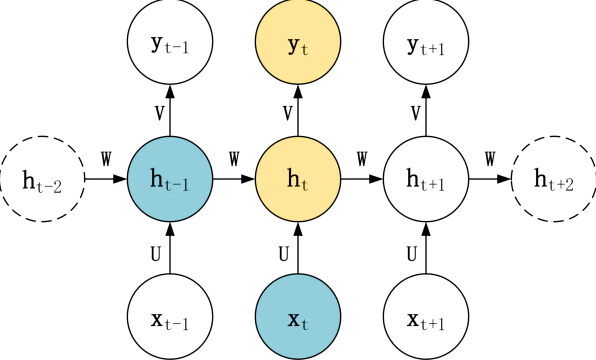
htyt=σ(zt)=σ(Uxt+Wht−1+b)=σ(Vht+c)
梯度消失与爆炸
假设一个只有 3 个输入数据的序列,此时我们的隐藏层 h1、h2、h3 和输出 y1、y2、y3 的计算公式:
h1h2h3y1y2y3=σ(Ux1+Wh0+b)=σ(Ux2+Wh1+b)=σ(Ux3+Wh2+b)=σ(Vh1+c)=σ(Vh2+c)=σ(Vh3+c)
RNN 在时刻 t 的损失函数为 Lt,总的损失函数为 L=L1+L2+L3⟹∑t=1TLT
t = 3 时刻的损失函数 L3 对于网络参数 U、W、V 的梯度如下:
∂V∂L3∂U∂L3∂W∂L3=∂y3∂L3∂V∂y3=∂y3∂L3∂h3∂y3∂U∂h3+∂y3∂L3∂h3∂y3∂h2∂h3∂U∂h2+∂y3∂L3∂h3∂y3∂h2∂h3∂h1∂h2∂U∂h1=∂y3∂L3∂h3∂y3∂W∂h3+∂y3∂L3∂h3∂y3∂h2∂h3∂W∂h2+∂y3∂L3∂h3∂y3∂h2∂h3∂h1∂h2∂W∂h1
其实主要就是因为:
- 对V求偏导时,h3是常数
- 对U求偏导时:
- h3里有U,所以要继续对h3应用
chain rule
- h3里的W,b是常数,但是h2里又有U,继续
chain rule
- 以此类推,直到h0
- 对W求偏导时一样
所以:
- 参数矩阵 V (对应输出 yt) 的梯度很显然并没有长期依赖
- U和V显然就是连乘(∏)后累加(∑)
∂U∂Lt=k=0∑t∂yt∂Lt∂ht∂yt(j=k+1∏t∂hj−1∂hj)∂U∂hk∂W∂Lt=k=0∑t∂yt∂Lt∂ht∂yt(j=k+1∏t∂hj−1∂hj)∂W∂hk
其中的连乘项就是导致 RNN 出现梯度消失与梯度爆炸的罪魁祸首,连乘项可以如下变换:
- hj=tanh(Uxj+Whj−1+b)
- ∏j=k+1t∂hj−1∂hj=∏j=k+1ttanh′×W
tanh' 表示 tanh 的导数,可以看到 RNN 求梯度的时候,实际上用到了 (tanh' × W) 的连乘。当 (tanh' × W) > 1 时,多次连乘容易导致梯度爆炸;当 (tanh' × W) < 1 时,多次连乘容易导致梯度消失。
- RNN (Private)
- 梯度消失 (Private)
- 梯度爆炸 (Private)
